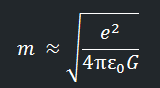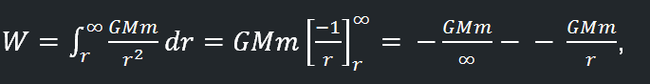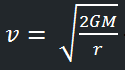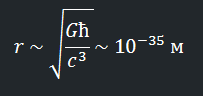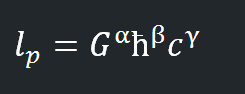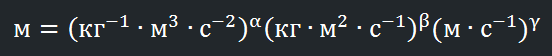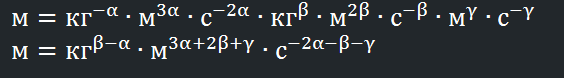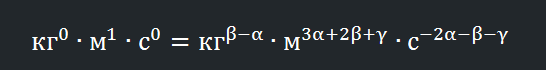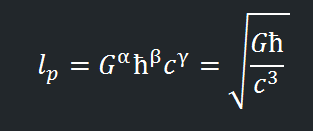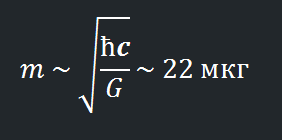Серия «Физика»

Система единиц измерения, используемая нами в повседневной жизни, вполне нас устраивает. Мы все имеем прекрасное представление о метре, килограмме, секунде. Тем не менее, людям, которые занимаются научными изысканиями, этого мало, так как зачастую они исследуют объекты либо слишком огромные, такие как галактики, либо слишком малые – такие как атомы. Действительно, хотя мы и можем выразить размеры любого объекта через метры, используя приставки, мы уже с трудом понимаем, чем, например, пикометр отличается от аттометра. Подавляющее большинство из нас даже не сможет сказать, что больше, а многие – вообще не слышали о таких приставках.

В 1899 году немецкий физик Макс Планк раздумывал, наверное, над чем-то подобным, потому и написал следующее:

Все до сих пор используемые системы единиц, в том числе так называемая абсолютная СГС-система, обязаны своим происхождением пока что случайному стечению обстоятельств, поскольку выбор единиц, лежащих в основе каждой системы, сделан не исходя из общей точки зрения, обязательно приемлемой для всех мест и времён, но исключительно исходя из потребностей нашей земной культуры…

Результатом его раздумий явилась работа, опубликованная в 1900 году, в которой он предложил систему единиц измерения…

…которые не зависели бы от выбора каких-либо тел или веществ и обязательно сохраняли бы своё значение для всех времен и для всех культур, в том числе и внеземных и нечеловеческих, и которые поэтому можно было бы ввести в качестве «естественных единиц измерений».

Макс Планк - герой этого поста

Забегая вперёд, скажу, что данный труд впоследствии был использован в большей части теоретической физики, а большинство общепринятых в настоящее время единиц измерения выведены напрямую из системы измерений, названных в его честь: Планковскими единицами.

До чего же он додумался? Предлагаю вместе пройти по пути его рассуждений.

Представим, что у нас есть пара электронов на расстоянии r друг от друга:

Что будет происходить, если бы мы начали сводить эту пару электронов всё ближе и ближе друг к другу?

1. Поскольку электроны обладают массой, между ними будет иметь место сила гравитационного притяжения, стремящаяся их сблизить.

2. Так же, мы знаем, что электроны имеют отрицательный электрический заряд, поэтому между ними будет иметь место электростатическая сила, расталкивающая их друг от друга.

Какая же из двух сил будет сильнее по мере их сближения (когда r → 0)? По закону всемирного тяготения, сила притяжения между двумя электронами будет выражена формулой:

Fg = G m₁ m₂ / r² – сила прямо пропорциональна произведению масс электронов и обратно пропорциональна квадрату расстояния между ними. В нашем эксперименте, m₁ и m₂ одинаковы и равны массе электрона, которую можно просто обозначить m, и переписать уравнение так:

Fg = G m² / r²

Сила электростатического расталкивания определяется по закону Кулона по такой формуле:

Fe = Q₁Q₂ / 4 πε₀ r² – эта сила прямо пропорциональна произведению двух зарядов и так же – обратно пропорциональна квадрату расстояния между ними. В данном случае, коэффициент пропорциональности задаётся ε₀ - электрическая постоянная (электрическая проницаемость вакуума). В нашем примере обе величины Q₁ и Q₂ равны e – заряду электрона, поэтому, формулу можно переписать так:

Fe = e² / 4 πε₀ r²

Посмотрим на отношение сил, чтобы понять, какая из них будет преобладать Fe / Fg = ? Запишем отношение:

Fe / Fg = e² / 4 πε₀ Gm²

Первое, что можно заметить, что r² сократилось, а это значит, что отношение двух сил никак не зависит от расстояния между двумя электронами и всегда будет одним и тем же (Хаха, нет! Но об этом позже). Зная значения всех элементов данного уравнения, подставив их и произведя расчёты, мы получим:

Fe / Fg = e² / 4 πε₀ Gm² ≈ 10⁴²

Иными словами, сила электростатического расталкивания превышает силу гравитации на 42 порядка! Чтобы полнее ощутить масштабы, запишу так:

Fe ≈ 1 000 000 000 000 000 000 000 000 000 000 000 000 000 000 * Fg.

Во столько раз гравитация слабее электромагнетизма, но именно гравитация была обнаружена первой. Почему? Потому что атомы, из которых состоит вещество, электрически нейтральны, положительный заряд протонов компенсируется отрицательным зарядом электронов. Из-за нейтральности атомов мы просто не замечали исключительно сильное электромагнитное взаимодействие. Гравитация – другое дело. Насколько можно судить сейчас, такой штуки как «отрицательная масса» не существует (во всяком случае, до сих пор никому не удалось обнаружить ничего похожего), поэтому два тела, обладающих массой, будут всегда испытывать взаимное притяжение.

Упрощённая Ньютоновская модель позволила нам сделать вывод о том, что отношение сил электростатического расталкивания и гравитации вообще не зависят от расстояния между двумя электронами, но, к сожалению, реальный мир не всегда так прост, как наши математические модели. Как обычно, её величество квантовая механика всё портит.

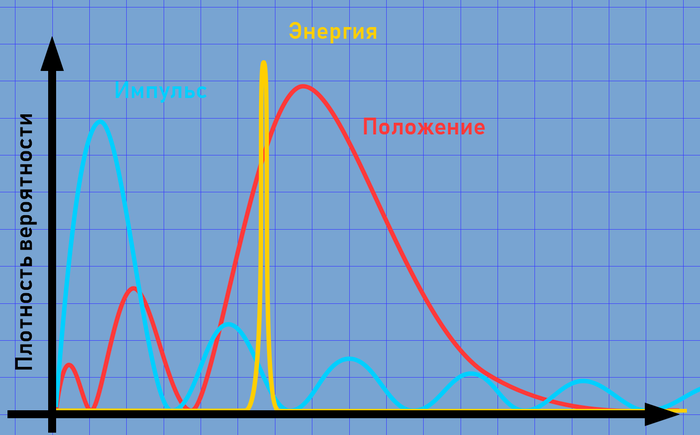
Чем меньше становится расстояние между электронами тем сильнее проявляется роль принципа неопределённости Гейзенберга (подробнее можно почитать в этом моём посте) – чем точнее мы пытаемся определить положение электронов в пространстве, тем сильнее разброс в их импульсах, тем больше они «дрожат», а чем сильнее эта «дрожь», тем выше их энергия. В какой-то момент, эта энергия становится достаточной для того, чтобы создать новый электрон (принцип эквивалентности массы и энергии А. Эйнштейна, знаменитое уравнение E = mc²). На самом деле мы можем легко посчитать расстояние между электронами, при котором наступят подобные условия, скомбинировав уравнение Эйнштейна с неравенством принципа неопределённости Гейзенберга.

Запишем уравнение таким образом: если мы ограничиваем объект в определённой области пространства размера ∆x, неопределённость в импульсе такого объекта ∆p должна быть примерно больше ħ / ∆x:

∆p ≳ ħ / ∆x

(ħ – редуцированная Планковская константа – просто коэффициент преобразования между энергией фотона и его частотой. На данном этапе достаточно понимать, что это константа).

В нашем случае с двумя электронами ∆x = r – расстояние между ними (∆p ≳ ħ / r).

Если импульс объекта растёт, очевидно, что растёт и энергия данного объекта, поэтому мы можем выразить энергию в данном выражении, умножив обе части на скорость света (с):

∆E ≳ ħ c / r

Кто сомневается, может вспомнить, что импульс – это произведение массы на скорость, а произведение единиц импульса (кг•м/с) на скорость (м/с) даст вам выражение единицы энергии (Джоуля) по определению (1 Дж = 1 Н•м=1 кг•м²/с²).

Из этого соотношения мы видим, что при уменьшении r, ∆E будет увеличиваться. Эта как раз энергия той квантовомеханической «вибрации», которую мы упускали из виду, используя уравнения классической механики. Теперь, имея на руках это соотношение, мы можем «прикинуть», какому расстоянию между электронами будет соответствовать энергия, достаточная для создания массы электрона по уравнению Эйнштейна (∆E ~ mc²), где m – масса электрона. Иными словами, нам нужен ответ на вопрос, когда соблюдётся отношение:

r ≲ ħ / mc

Подставив известные значения констант и массы электрона, мы получим:

ħ / mc ≈ 10⁻¹³ м

Это расстояние меньше среднего размера атома, которое составляет примерно 10⁻¹⁰ м, но сильно больше размера ядерного ядра (10⁻¹⁵ м). Иными словами, полученная величина говорит нам о том, что если мы попытаемся сблизить два электрона на расстояние, меньшее 10⁻¹³ м, квантовая неопределённость в их энергии будет достаточной для создания нового электрона. То есть, на этом расстоянии уже нельзя пренебрегать ни квантовой механикой, ни теорией относительности.

Но что будет, если мы будем продолжать сближать электроны друг к другу? Мы уже убедились, что согласно Гейзенбергу, с уменьшением расстояния ∆x растёт энергия ∆E, а согласно Эйнштейну, это эквивалентно добавлению массы в нашу систему. А раз гравитация у нас взаимодействует с массой, то расти будет и Fg (гравитационное притяжение между электронами)? С ростом массы, соотношение сил электростатического расталкивания и гравитационного притяжения уже не будет оставаться неизменной величиной, посчитанной нами ранее (10⁴²).

И так, следующий вопрос, на который нам надо найти ответ – при какой расстоянии между электронами гравитационное притяжение станет сравнимым с электростатическими силами, расталкивающими заряды по закону Кулона?

Для этого, мы просто должны выяснить, при каком значении m, выполнится данное условие:

Fe / Fg = e² / 4 πε₀ Gm² ≈ 1

Преобразуем уравнение к следующему виду:

Теперь, это значение массы можно преобразовать к энергии и подставить в выражение принципа неопределённости. После всех преобразований, получим:

r ≲ ħ / mc ≈ 10⁻³⁴ м

На этом расстоянии, гравитационное притяжение между электронами уравновесит силу их электростатического расталкивания, но что произойдёт, если мы продолжим уменьшать расстояние между электронами? Разумеется, гравитационное взаимодействие будет только увеличиваться, но будет ли это продолжаться всегда?

Оказывается, что нет. В дело снова вступит теория относительности и предъявит свой самый эффектный козырь – чёрную дыру. Здесь нужно чуть отвлечься от наших электронов и разобраться, какие условия вообще способствуют образованию чёрной дыры.

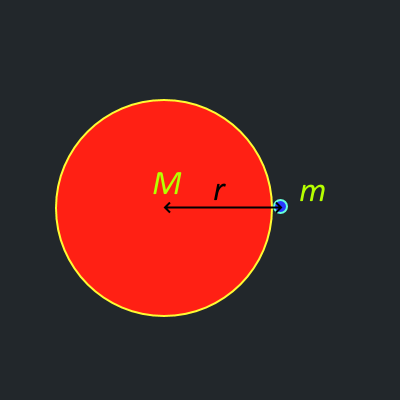
Давайте рассмотрим тело с малой массой m, расположенное на поверхности большего тела с массой M.

Между этими двумя телами действует сила гравитационного притяжения, выраженная формулой:

F = G Mm / r²,

… и, чтобы оторвать малое тело от поверхности большого, мне необходимо совершить работу по преодолению этой силы. Если я удалю малое тело от большого на некоторое расстояние dr, я совершу работу:

dW = F dr = (GMm / r² ) dr

Но если мне потребуется понять, какую работу мне необходимо совершить, чтобы удалить малое тело на бесконечно большое расстояние, так как сила притяжения между двумя телами будет убывать обратно пропорционально квадрату расстояния между этими двумя телами – надо будет проинтегрировать:

чтобы убедиться, что полная работа будет равняться:

W = GMm / r

По мере удаления m от M, тело будет набирать потенциальную энергию, и полная величина этой потенциальной энергии будет равняться полной проделанной работе.

Вооружившись этим знанием, я могу задаться вопросом, с какой скоростью мне надо подбросить m, чтобы оно вырвалось из области гравитационного притяжения M. Или, если перефразировать: какую скорость надо придать m, чтобы оно смогло удалиться на произвольно большое (бесконечное) расстояние от M?

Поскольку я только что посчитал, какая энергия необходима для этого, мне достаточно сообщить m такую же кинетическую энергию. Зная формулу кинетической энергии, получаю:

½ mv² = GMm/r

Решаем уравнение в отношении v (скорости) и получаем:

в русскоязычной терминологии эта скорость получила название «Вторая космическая скорость» (скорость освобождения или скорость убегания). Для Земли эта скорость составляет приблизительно 11 км / с, а, например, для Юпитера – уже около 60 км / с.

Из формулы видно, что вторую космическую скорость определяют два фактора – масса тела и его радиус – большая скорость освобождения требуется не только при старте с массивного объекта, но и с более плотного (чем в меньший объём «упакована» масса, тем сложнее с неё улететь).

И следующий вопрос, которым может озадачиться пытливый ум – а что случится, если объект будет настолько плотным, что вторая космическая скорость для него сравняется со скоростью света? Такие объекты получили название «чёрная дыра», так как даже свет не может покинуть их окрестности. Уже зная формулу, мы можем просто подставить в уравнение скорость света и решить его для любой массы (плотности), а преобразовав его для r – получим уравнение радиуса, внутрь которого необходимо «упаковать» массу M, чтобы образовалась чёрная дыра:

Rs = 2GM / c²

Эту величину называют «Радиусом Шварцшильда», в честь немецкого физика Карла Шварцшильда, который впервые решил уравнения Эйнштейна для такого случая и, тем самым, предсказал существование чёрных дыр.

Так какое отношение это всё имеет к нашим электронам? Самое непосредственное. Мы уменьшаем расстояние между ними, масса системы растёт, а размеры уменьшаются. Рано или поздно мы «упакуем» их достаточно плотно, так, чтобы в этой области пространства сформировалась чёрная дыра. А, имея необходимые формулы, мы можем вычислить, когда это произойдёт.

Во-первых, мы можем оценить, сколько гравитационной массы содержится в системе из двух электронов на расстоянии r друг от друга (r ~ ħ / mc). И так же, мы только что посчитали, как радиус Шварцшильда связан с гравитационной массой (r ~ Gm/c²). Объединив эти два уравнения, мы увидим, что m сократится, а всё, что останется можно записать следующим образом:

Что примечательно, если внимательно приглядеться к этой формуле, можно заметить, что она целиком состоит из констант и никак не содержит никаких других параметров. Мы можем взять не только электроны, но и любые иные два объекта, и если мы уменьшим расстояние между ними до 10⁻³⁵ м, в данном объёме неизбежно возникнет чёрная дыра и на этом этапе мы больше не сможем извлечь никакой дополнительной информации из системы. Даже если вы захотите «вкачать» в систему ещё больше энергии, это приведёт лишь к росту этой чёрной дыры.

Мы подошли к фундаментальному пределу, точнее которого мы физически не в состоянии ничего измерить. Данный предел, по фамилии его первооткрывателя носит название Планковская длина. Это граница, где заканчиваются даже наши теоретические возможности познания пространства. Примечательно, что на данном пределе и квантовая механика и теория относительности становятся одинаково важны.

Тут человек, знающий историю научных открытий, может спросить – но ведь Планк опубликовал свои труды раньше, чем Эйнштейн опубликовал свою теорию относительности, да и до открытия принципа неопределённости было ещё далеко!

Поэтому сейчас мы пройдём по пути, пусть менее наглядному, но доступному Максу Планку в самом конце 19 века.

В наших выкладках можно увидеть постоянное использование 3 разных констант из трёх областей физики. Мы использовали постоянную Планка-Дирака (E = ħω) , основную константу квантовой механики; так же – скорость света (E = mc²), основную константу общей и специальной теории относительности, а так же Ньютоновскую универсальную гравитационную константу (F = G (m1m2 / r²). Здесь можно задаться вопросом – каковы фундаментальные, базовые единицы измерения для этих трёх констант?

Все возможные единицы измерения являются производными от 7 базовых:

Расстояние – метр, м

Время – секунда, с

Масса – килограмм, кг

Электрический ток – Ампер, А

Количество вещества – моль

Интенсивность света – канделла, Кд

Температура – кельвин, К

(четыре последних нас сейчас не интересуют, они приведены просто для комплекта)

Любая другая величина выражается через использование этих семи. Например, скорость выражается как расстояние, преодолённое за время (метры в секунду, м/с), ускорение будет выражено как изменение скорости за единицу времени (метры в секунду за секунду или м/с²)

Как же выражаются используемые константы скорости света, гравитационной постоянной и постоянной самого Планка?

Скорость света (с) – это просто – м/с.

Постоянная Планка-Дирака (ħ) уже сложнее – исходя из определения, видно, что она имеет в себе единицы энергии, разделённые на частоту ħ = E / ω, где в числителе мы имеем энергию (Джоуль – это сила * расстояние, или 1 Дж = 1 Н•м=1 кг•м²/с²), а в знаменателе – частоту ([ω] = [2πf]) = Гц (раз в секунду или с⁻¹). Совместив единицы, мы получаем единицы измерения постоянной Планка (ħ): кг*м²/с.

Ну и гравитационная постоянная (G) выражается следующим образом:

Теперь, зададимся вопросом, а можем ли мы при помощи этих констант выразить длину?

Именно этот вопрос задал себе Макс Планк более 100 лет назад. Можно ли при помощи этих трёх фундаментальных констант создать новую единицу измерения длины? Трюк, который он придумал – записывать их как произведение G в какой-то степени α, ħ в какой-то степени β и с в какой-то степени γ:

Тогда его задача сводилась к определению степеней α, β и γ, таким, чтобы комбинации:

[c] = м с⁻¹

[ħ] = кг м² с⁻¹

[G] = кг⁻¹ м³ с⁻²

сводились бы просто к метрам.

Упрощаем:

Теперь, запишем левую часть уравнения в более подходящей форме:

Ну и теперь нам нужно просто сопоставить степени в левой и правой части уравнения, получив следующую систему:

0 = β – α

1 = 3 α + 2 β + γ

0 = –2α -β – γ

Первое уравнение говорит нам, что α = β, зная это , получаем:

1 = 3 α + 2 β + γ → 1 = 5 α + γ

0 = –2α -β – γ → 3 α = – γ

Следовательно, имеем α = 1/2 , β = 1/2, γ = – 3/2

Подставив значения степеней в формулу, мы обнаружим, что мы получили то же самое уравнение, что и раньше:

Планк не остановился на этом. Мы так же можем посчитать, а сколько массы нужно упаковать в этот объём, чтобы получить чёрную дыру. Нам всего только надо преобразовать полученное уравнение:

Эта величина получила название «Планковская масса».

Есть так же «Планковское время» – строго говоря, время, за которое свет проходит расстояние равное «Планковской длине» (5,3 * 10⁻⁴⁴ с), но у этой величины есть и другое значение. Помимо того, что это – кратчайший интервал времени, который в принципе имеет физический смысл, это так же и кратчайший интервал, дальше которого мы никогда не сможем проникнуть в исследовании условий большого взрыва. Период с момента возникновения нашей Вселенной до 5,3 * 10⁻⁴⁴ с так и называется – Планковская эпоха.

Концепция самого времени теряет физический смысл на интервалах, меньше планковского времени!

Очень часто можно слышать вопрос «А что было до Большого взрыва?». Правда в том, что время не существовало как концепция на протяжении всей Планковской эпохи, как и не существовало никаких «до» (см. пост Правды и кривды теории Большого взрыва.).

Теперь, уткнувшись в столь фундаментальный барьер, мы можем только гадать, является ли пространство-время непрерывным на любом интервале, мы лишь не можем ничего измерить на расстояниях, меньших Планковских, либо пространство-время дискретно, имеет «воксели» – мельчайшие кирпичики, и тогда самым наглядным аналогом подобной реальности станет популярная игра Minecraft, а пространства-времени в меньшем масштабе попросту не существует.

С объяснением вроде того, что угол падения равен углу отражения, с неровных поверхностей свет отражается под разными углами и рассеивается, зато вот с гладких поверхностей все лучи света отражаются под одним и тем же углом. Это правило вытекает из принципа, который сформулировал ещё Христиан Гюйгенс в конце 17 века, и дополнил Огюстен Френель в начале 19. Каждая точка фронта (поверхности, достигнутой волной) является вторичным (то есть новым) источником сферических волн (принцип Гюйгенса-Френеля).

То же в анимации:

Но почему вот, например, относительно гладкий лист бумаги нам видится белым, а весьма шершавый кусок железосодержащей породы обладает, как мы говорим «характерным металлическим блеском». И почему существуют прозрачные материалы, которые пропускают свет сквозь себя практически без изменений?

Металлический блеск

Опустимся ещё глубже. Предметы состоят из атомов, так, наверное, это «одни атомы отражают, а другие пропускают сквозь себя лучи света»? (Физики, не спешите кидать в меня камни, я исправлюсь, обещаю!). При этом, какие-то лучи будут отражаться от внешних атомов, а какие-то будут проникать между ними и попадать в атомы, лежащие в более глубоких слоях:

При этом, может сложиться так, что лучи света будут отражаться даже внутрь материала. И да, я ещё пока не упоминал волновую природу света. Абсолютно любой материал, без исключения, будь то зеркало, камень или стекло разделит падающий луч света на 2 неравные части — одна часть будет отражена, а вторая будет направлена внутрь материала. При этом, вторая часть может быть как поглощена данным материалом, так и пройти сквозь него практически без изменений.

Для стекла, лишь малая толика света будет отражена, большая же часть пройдёт сквозь него. Для зеркала всё с точностью «до наоборот». То, насколько глубоко в материал проникнет свет, зависит, в основном, от 4 вещей: магнитной проницаемости материала, его диэлектрической проницаемости, частоты падающего излучения и, наиболее важного фактора — удельного электрического сопротивления материала. Так, например, в стекле (электрический изолятор) интенсивность светового пучка упадёт ниже 1% от первоначального примерно через 750 метров. Для серебряной амальгамы (отлично проводящей электрический ток) эта глубина составит всего около 7 нанометров (несколько десятков атомов). Комбинируя данные параметры можно создать и более экзотические материалы (о метаматериалах я писал в этом посте).

Интересующимся — формула:

Но тогда почему не все изоляторы прозрачны? Есть ещё один фактор, но для этого, надо нырнуть ещё глубже. Вспоминаем, что фотон — это волна, а не мячик, который может отскочить от поверхности. Фотон движется прямолинейно и не может изменить своей траектории относительно геодезических линий пространства(времени). Фотон никуда не отражается. Любой материальный объект (включая зеркало) может лишь поглотить падающий фотон, либо пропустить его сквозь себя.

Так что же происходит на самом деле? Давайте вспомним, как происходит взаимодействие атомов с квантами электромагнитного излучения (подробно разжёвано здесь). Каждый электрон в атоме находится в состоянии, которое можно описать 4 квантовыми числами, а если проще — имеет определённую энергию. Чем больше энергия, тем дальше от ядра она позволяет ему находиться, но есть одно условие — электрон не может находиться на произвольном расстоянии от ядра, как в здании с лифтом — нельзя находиться на этаже 3 ½, можно либо на 3, либо на 4, но не между ними. «Этажи» называются орбиталями и переход с одной на другую осуществляется мгновенно, без каких-либо промежуточных стадий. Если фотон с совершенно определённой энергией встретится с электроном, он будет поглощён, а его энергия позволит электрону подпрыгнуть на этаж выше. Про такой электрон говорят, что он возбуждён. Рано или поздно, возбуждённый атом «успокоится» и вернётся в исходное состояние, а, поскольку для этого необходимо будет отдать энергию, он отдаст её в виде нового фотона, у которого будет точно такая же энергия (частота) как и у поглощённого фотона. Но если энергии фотона будет недостаточно для того, чтобы электрон перескочил на следующую орбиту, то он просто пролетит мимо, а электрон останется на свой орбите. Также электрон останется на орбите и в случае, если фотон имеет слишком большую энергию. Для перехода электрона на другой уровень фотон должен обладать совершенно определенном количеством энергии.

Поглощение и эмиссия фотонов

Определённые материалы прозрачны для определённой частоты излучения (как, например, стекло) из-за того, что энергии фотонов видимого диапазона недостаточно, чтобы возбудить электроны в атомах стекла, поэтому фотоны спокойно проходят сквозь них. При этом, один и тот же материал может быть прозрачным в одном диапазоне и непрозрачным в другом — так, например, стекло очень хорошо поглощает ультрафиолет.

Но данный механизм отвечает лишь за нагрев материала, на который попадает свет, так как перевыпущенный фотон будет, скорее всего, поглощён соседним атомом, через какое-то время, снова перевыпущен, и так дальше. Так светится нагретый металл, например. Исключением из этого правила может быть лишь такие явления как флуоресценция или фосфоресценция, когда интенсивность свечения материала значительно превышает интенсивность теплового излучения.

Флуоресценция уранового стекла в ультрафиолете

Для объяснения физики отражения нам, оказывается, вовсе не нужна квантовая механика, всё объясняется вполне классическим эффектом. Свет является электромагнитной волной, а сам атом имеет два электрических заряда — положительный в ядре и отрицательный в электронах. Что мы знаем о зарядах в магнитном поле? Они движутся под действием силы Лоренца. Атом начинает вибрировать с той же частотой, что и попадающий в него свет. А поскольку вибрация — это движение с ускорением, вспомним, что делает электрический заряд, движущийся с ускорением? Он начинает испускать фотоны. Именно эти фотоны и формируют отражённую электромагнитную волну.

При этом, разумеется, каждому отдельному атому и фотонам, которые ими испускаются, глубоко наплевать на правило «угол падения равен углу отражения». Излучение испускается во всех направлениях сразу. Только согласно принципу Гюйгенса-Френеля мы получаем в зеркале отражённое изображение.

На формирование отражения влияет множество факторов — расстояние между атомами, интервалы времени между поглощением и перевыпуском фотонов, резонансные частоты и многое другое. Чтобы не заморачиваться со всеми этими параметрами, люди объединили их влияние в один параметр — индекс рефракции. Его посчитали для всех известных материалов и занесли в таблицы и теперь при расчётах, связанных с оптическими системами, мы можем просто забыть об атомах и молекулах, достаточно знать лишь тип материала. Разумеется, каждый материал имеет индивидуальные характеристики поглощения и отражения для света разных частот, именно эта особенность материалов отвечает за наше восприятие цвета.

Подводя итог — свет на самом деле не отражается от зеркала. Зеркало поглощает падающий на него свет и испускает новый, точно такой же.

Теория Большого взрыва уходит корнями в глубокое прошлое. Среди философов и позднее – религиозных деятелей шёл спор, была ли Вселенная всегда (как утверждал Аристотель) или у неё было начало (что больше устраивало ранних иудеев). В 1225 году в своём трактате «О свете и о начале форм», английский теолог Роберт Гроссетест описывал рождение Вселенной во взрыве с последующей кристаллизацией материи, из которой образовались звёзды и планеты, заняв своё место на небесных сферах вокруг Земли. В 18 веке Эразм Дарвин (дед более известного Чарльза Дарвина) описывал циклически расширяющуюся, а затем – сжимающуюся вселенную. Эдгар По в своей «Эврика. Поэма в прозе», описал начало Вселенной из «первозданной частицы… по божьей воле». Согласно По, «божья воля» проявилась в расталкивающей силе, разделившей первозданную частицу на атомы. Атомы распределились в пространстве, после чего расталкивание прекратилось, и началось притяжение, в результате которого материя начала собраться в звёзды и планеты.

В начале 20 века с использованием спектроскопии удалось обнаружить красное смещение в спектрах удалённых «спиральных туманностей» (тогда их ещё не называли галактиками). На то время было сложно объяснить это явление, так как считалось, что небесные объекты размещены во вселенной более-менее стационарно.

Красное смещение первым объяснил, не Эдвин Хаббл, а Жорж Леметр (католик и иезуит). Его объяснение гласило: Вселенная не статична, а расширяется. Через два года американец Эдвин Хаббл повторил открытие и выявил закономерность, согласно которой величина красного смещения возрастает пропорционально расстоянию до объекта, это открытие назвали законом Хаббла.

В 1931 году Леметр предложил «гипотезу первобытного атома», от взрыва которого и началась Вселенная. Сам термин «Большой взрыв» (Big bang) создал, по иронии судьбы, противник теории взрыва, Фред Хойл, который предлагал альтернативное объяснение красного смещения в своей теории стационарной вселенной. Согласно ней, между разлетающимися галактиками постоянно создаётся новая материя. Хойл выступал с лекциями по третьему каналу Би-Би-Си, и, высмеивая теорию своего оппонента, ввернул фразу «…эта идея большого взрыва» (that ‘big bang’ idea).

Две теории конкурировали между собой. Обе теории могли объяснить происхождение вселенной, но теория стационарной вселенной не могла объяснить её текущее состояние. Почему, например, квазары и радиогалактики наблюдаются астрономами гораздо чаще только на больших от нас расстояниях, а рядом с нами их нет. Наконец, в 1964 году, произошло открытие, окончательно похоронившее теорию стационарной вселенной и буквально перевернувшее мир физики. Сотрудники лаборатории Белла Арно Пензиас и Роберт Вилсон при помощи такой вот рупорной антенны занимались поиском источников радиоизлучения, которые потенциально могли навредить космическим спутникам:

При калибровке установки они никак не могли избавиться от «шума» – статических помех. Куда бы они ни направляли свою антенну, отовсюду они получали помехи в микроволновом диапазоне электромагнитного излучения. Такой сигнал могло бы излучать тело, имеющее температуру 2,7 Кельвин (это чуть выше абсолютного нуля). Сигнал можно было получить с любого направления, он был буквально везде, будто бы источник этого излучения находился на внутренней стороне сферы, в центре которой мы находимся? Что же за источник у этого «света»?

Все, наверное, видели лампу накаливания или нагретый докрасна металл (например, в тостере). Это не отражённый свет, этот свет испускается самими атомами вещества (подробнее о механизме см. Как выглядит атом?). Учёные пользуются термином «абсолютно чёрное тело» – это идеализированная модель объекта, который поглощает всё электромагнитное излучение, падающее на него, не отражая ничего, и может испускать только собственный свет, длина волны которого зависит только от его температуры. Если построить график интенсивности излучения такого тела, в зависимости от его нагрева, то получится что-то вроде этого:

Свой спектр теплового излучения, в той или иной степени походящий на спектр излучения абсолютно чёрного тела, имеет любой объект в нашей Вселенной. Если мы опустим температуру тела до 2,7 К, то пик интенсивности сдвинется из видимого диапазона в микроволновый, а спектр в точности совпадёт со спектром наблюдаемого радиоастрономами излучения. И когда я говорю «в точности», это не фигура речи. Спектр открытого излучения в действительно в точности совпадал с математической идеальной моделью.

Мы знаем, что вселенная пуста, там ничего нет, что могло бы иметь температуру, да к тому же ещё и вполне определённую температуру 2,7 К. Почему открытое излучение вообще имело тепловой спектр?

Так было открыто реликтовое микроволновое излучение. По сути, Пензиас и Вилсон «увидели свет» от Большого взрыва – процесс, в ходе которого сформировались первые атомы во Вселенной около 13,5 миллиардов лет назад.

Мы знаем, что вселенная расширяется, это подтверждается красным смещением в спектре удалённых от нас объектов. Чем дальше объект от нас, тем длиннее волна дошедшего до нас излучения.

Единственное объяснение этому в рамках общей теории относительности – то, что расширяется само пространство. Чем больше расстояние, пройдённое светом, тем больше его волна будет «растянута». Мы можем использовать уравнения общей теории относительности (ОТО) и «отмотать» время назад, чтобы построить модель ранней вселенной. Согласно ОТО, получается, что когда-то вселенная умещалась в точку бесконечно малого размера – сингулярность, в момент времени t = 0, гипотетическое начало существования нашего мира.

Не все космологи склонны слепо доверять ОТО в данном случае. Дело в том, что, хотя данная теория с успехом объясняет наблюдаемые явления и предсказывает результаты научных экспериментов, она не в состоянии смоделировать квантовое состояние гравитации в этот первичный момент времени. Мы знаем, что на каком-то моменте нашей «перемотки» времени, чистая ОТО начнёт давать неверные предсказания, так как состояние вселенной на тот момент времени выйдет за рамки сферы применимости ОТО. Эти ограничения давно известны физикам и не являются чем-либо выдающимся, так что не спешите кричать о том, что Эйнштейн был неправ. Мы можем достоверно судить о состоянии Вселенной после Большого взрыва только с определённого момента.

С точностью мы можем сказать, что когда-то Вселенная была очень плотной, очень горячей, а также – непрозрачной. Где-то в возрасте 370 тыс. лет она была оранжевого цвета. В эту эпоху она была наполнена плазмой из хаотично движущихся заряженных частиц и имела температуру в несколько тысяч градусов. Это слишком большая температура для того, чтобы электроны и протоны могли сформироваться в атомы. Эта плазма излучала свет (как и любое другое нагретое вещество), однако, фотоны этого света не могли распространяться далеко из-за большой плотности вещества. Испускаемые фотоны просто сталкивались с каким-либо электроном и, либо снова поглощались, либо отскакивали как бильярдные шары. Внутри этой плазмы была практически нулевая видимость.

Но Вселенная расширялась, а плазма, соответственно, постепенно охлаждалась и настал момент, когда её температура опустилась ниже 3000 К.

Цветовая температура в 3000 К соответствует оранжевому цвету. Забавно, что художники считают более «тёплыми» цвета лампочек слева и более «холодными» – справа, хотя физически дела обстоят совсем наоборот.

При этой температуре, наконец, смогли образоваться нейтральные атомы, и свободных электронов практически не осталось. Плазма превратилась в горячий газ, а вселенная впервые стала прозрачной для электромагнитного излучения. Испущенные в этот миг фотоны уже не встречали на своём пути препятствий, и устремились во все стороны сразу. Свет этих фотонов путешествует и по сей день, но первоначально оранжевый, он со временем всё больше и больше подвергался действию красного смещения, его спектр краснел, затем перешёл в инфракрасную область спектра, а затем – в микроволновую. К настоящему моменту этот свет «остыл» до 2,7 К и фиксируется только при помощи радиотелескопа.

На рисунке ниже показаны карты реликтового излучения, где микроволновый диапазон сдвинут область видимого спектра. Надо иметь в виду, что хотя излучение и показано на подобных иллюстрациях контрастными цветами, в действительности, разница между самым холодным пятном и самым горячим составляет всего 0,8 мкК (восемь миллионных долей градуса).

Вы тоже можете увидеть его, просто включив ненастроенный телевизор. Около 1% помех на экране вашего телевизора вызваны фоновым реликтовым излучением.

Важность открытия реликтового излучения огромна для теории Большого взрыва. Наличие этого излучения можно объяснить только тем, что когда-то Вселенная была меньше, плотнее и горячее, чем сейчас.

Неравномерность излучения (пусть и выражающиеся в температурах порядка одной тысячной градуса) позволяют судить о «местах», где сформировались звёзды, галактики и галактические скопления. Чем дальше мы смотрим в космическое пространство, тем моложе эпоха, которую мы наблюдаем. Мы можем наблюдать первые галактики, сформировавшиеся сразу после Большого взрыва. Теория подсказывает нам, что мы должны наблюдать бурные процессы столкновений и слияний галактик, богатых веществом для образования звёзд, но бедных в части тяжёлых элементов, образующихся только в результате взрывов сверхновых (см. Вскрываем трупы звёзд). И астрономы наблюдают в точности такую же картину, что и предсказывает теория. Самые дальние галактики, образовавшиеся в первые 5% времени существования вселенной, выглядят совершенно не так, как галактики, более близкие к нам. Вселенная определённо эволюционирует!

Если теория Большого взрыва верна, видимая «рябь» в волнах реликтового излучения должна нести в себе «отпечаток» распределения материи в момент, когда фотоны реликтового излучения отправились в путь, и такой же рисунок должен повторяться в распределении галактик на небе.

В рамках большого Слоановского цифрового обзора неба SDSS-III (Sloan Digital Sky Survey-III) в 2014 был проведён спектроскопический обзор барионных колебаний (BOSS/ Baryon Oscillation Spectroscopic Survey). Были измерены незначительные повторяющиеся изменения плотности галактик на расстоянии до шести миллиардов световых лет от Земли (что соответствует красному смещению 0,7), когда возраст Вселенной был равен примерно половине текущего. Эти волны, вариации плотности галактик известны как барионные акустические колебания. В определённом смысле, мы можем не только «видеть» большой взрыв, но и «слышать» его.

https://www.nanowerk.com/news2/space/newsid=35104.php

Все эти эксперименты пока что позволили нам узнать, что происходило во Вселенной, начиная с «возраста» примерно в 400 тыс. лет, и заканчивая настоящим моментом (примерный возраст Вселенной – 13,5 млрд. лет).

Используя эксперименты на ускорителях и моделируя раннюю Вселенную, мы можем с уверенностью предсказать её развитие и в непрозрачную эпоху. В возрасте нескольких секунд Вселенная была гораздо горячее, чем звёздное ядро. В таком состоянии она находилась примерно 20 минут. В этот период активно проходил первичный нуклеосинтез – формировались ядра первых атомов.

Теория Большого взрыва позволяет нам предсказать температуру и длительность этой фазы. Мы можем судить об этом по наблюдаемому распределению водорода и гелия в наблюдаемой Вселенной (водород ~75%, гелий-4 ~25, дейтерий и гелий-3 меньше 0,01%). Именно столько гелия должно было синтезироваться за 20 минут времени.

Условия ранней вселенной, которые мы смогли повторить на Земле в Большом адронном коллайдере, позволяют нам с уверенностью судить о развитии Вселенной, начиная с возраста 10⁻³² секунды, когда вся наблюдаемая Вселенная была размером с песчинку. Мы смогли убедиться, что наши модели по-прежнему работают и при таких высоких энергиях.

При температурах порядка 1 квадриллиона градусов, поле Хиггса перестаёт работать. Поле Хиггса даёт частицам их массу покоя, и если его убрать, то частицы-переносчики слабого фундаментального взаимодействия – бозоны W⁺, W⁻ и Z⁰ становятся неотличимы от фотонов. Это означает, что слабое и электромагнитное взаимодействия при таких условиях объединяются в одно – электрослабое. Период времени, когда такие условия имели место, называется электрослабая эпоха.

Эти условия мы ещё можем воспроизвести, на БАК, но когда температура превышает 10²⁹ К и возрасте Вселенной 10⁻³⁸ секунды, наша уверенность в чём-либо заканчивается, так как воспроизвести подобные условия на Земле мы не можем.

Мы можем только предполагать, что на этом этапе электрослабое взаимодействие и сильное ядерное взаимодействие так же объединяются в одно. Существует несколько идей того, как это могло бы происходить, и все эти теории получили общее название теории великого объединения. По правде говоря, их проще назвать гипотезами, так как неизвестно, какая из них верна (если вообще среди них есть верные). Для их проверки требуются уровни энергии, в триллионы раз превышающие те, что мы могли достичь в Большом адронном коллайдере. Может, оно и к лучшему, что подобная энергия нам пока недоступна.

Отмотаем время ещё немного, до возраста 10⁻⁴² секунды. В этот момент, видимая нам Вселенная имела размеры 10⁻²⁰ диаметра протона – этот размер называется Планковской длиной (1,6⋅10⁻³⁵ м). И на этом рубеже, вся известная нам физика попросту перестаёт существовать. Общая теория относительности вступает в серьёзный конфликт с квантовой механикой, так как четвёртое фундаментальное взаимодействие – гравитация начинает выдавать в уравнениях одну сингулярность за другой.

Для объяснения того, что происходило в этот момент нам необходима теория квантовой гравитации, которую ещё называют «Теорией Всего», так как в её рамках действительно можно будет объяснить любой наблюдаемый процесс во Вселенной.

Вернёмся снова к моменту, когда Вселенная стала прозрачной. Её возраст составляет примерно 400 тыс. лет, её размер примерно в 1000 раз меньше её текущих размеров. Как уже было сказано, мы можем наблюдать последний свет большого взрыва в виде реликтового микроволнового излучения, однако учёным до сих пор непонятно, почему его температура настолько равномерна – она колеблется в пределах одной стотысячной градуса, будто бы всё вещество в остывающей Вселенной было тщательно перемешано. Все мы видели, как сливки смешиваются с кофе со временем, даже если их специально не перемешивать, но проблема в том, что, основываясь только на уравнениях ОТО, у расширяющейся Вселенной не было времени на то, чтобы так перемешаться до настолько однородного уровня.

Чтобы две подсвеченные области на рисунке могли прийти к тепловому равновесию, должно быть «что-то», что бы переместилось от одной области к другой и не передало энергию. Но ничто в этом мире, даже свет, не успело бы пройти данное расстояние за отведённое моделью время.

Даже если мы возьмём вселенную, размером с песчинку и возраст вселенной 10⁻³² сек., и возьмём фотон, испущенный у одного края этой песчинки, затем применим скорость расширения вселенной и умножим всё это на 400 тыс. лет, то мы поймём, что фотон просто не успевает долететь до противоположного края. Расстояние между краями нашей «песчинки» будет увеличиваться быстрее скорости света. Иными словами, противоположные края Вселенной всегда находились вне горизонта частиц друг друга. Проблему так и назвали «Проблемой горизонта».

Единственным на сегодняшний день объяснением данной проблемы является гипотеза о том, что Вселенная была изначально достаточно малого размера, чтобы «перемешаться» как следует и достичь однородности, а затем резко раздуться в размерах со скоростью, которая значительно превышает скорость, предсказанную ОТО. Данная теория получила название «инфляционная модель».

Идея в том, что Вселенная началась с субатомных размеров, имела достаточно времени, чтобы прийти к термодинамическому равновесию, а затем вошла в стадию экспоненциального взрывного роста в размерах (инфляции), в ходе которого увеличилась по меньшей мере в 10²⁶ раз, после чего расширение замедлилось до текущих темпов. Таким образом, её края были вырваны из конусов причинно-следственных связей друг друга. Данная идея объясняет Проблему горизонта, однако оставляет вопросы относительно того, что послужило причиной взрывного роста и почему потом этот рост замедлился. Тем не менее, инфляционная модель настолько хорошо объясняет столько всего, что большинство космологов соглашается с тем, что что-то подобное должно было иметь место, хотя никаких свидетельств этому нет.

В этом свете Теорию Большого взрыва стоит рассматривать не как теорию образования нашей Вселенной, а как теорию объясняющую период расширения от субатомных размеров до космических. Некоторые аспекты данной теории имеют настолько жёсткие подтверждения, что не оставляют сомнений в верности «общей картины», однако, как и у любой теории, у Теории Большого взрыва есть границы применимости. Может быть, мы сможем дополнить эту теорию, а может – процесс познания Вселенной проведёт нас гораздо дальше Большого Взрыва.

В завершении я хочу развеять несколько распространённых заблуждений, которые встречаются у людей, поверхностно знакомившихся с теорией большого взрыва:

Миф: Теория Большого взрыва описывает начало существования нашей Вселенной. На самом деле, сама теория Большого взрыва ничего не говорит о непосредственном рождении Вселенной. Текущая концепция подразумевает существование энергии, времени и пространства, и не объясняет их происхождения.

Миф: Большой взрыв был «крохотным». Многие, пытаясь визуализировать большой взрыв (я – не исключение), пытаются сравнивать Большой взрыв с повседневными объектами. Это сравнение, однако, верно только в части Наблюдаемой Вселенной, а не всей Вселенной.

Миф: Закон Хаббла нарушает специальную теорию относительности. Действительно, дальние галактики удаляются от нас быстрее скорости света. Однако, специальная теория относительности применима только к движению сквозь пространство. В данном случае, расширяется само пространство.

Миф: Красное смещение удаляющихся галактик вызвано эффектом Доплера. Астрономы часто ссылаются на космологическое красное смещение, будто это обычный эффект Доплера. Хотя они схожи по своему действию, у них разный механизм. Доплеровское красное смещение основано на специальной теории относительности, которая не принимает во внимание расширение пространства. Космологическое же красное смещение основано на общей теории относительности, которая учитывает расширение. Для относительно близких к нам галактик, они могут показаться идентичными, однако, если пытаться описать красное смещение далёких галактик эффектом Доплера, можно прийти к неверному результату.

Внутри звёзд идёт постоянная борьба бобра с ослом фундаментальных сил природы, поэтому для правильной постановки диагноза, надо понять, что происходит.

Ггггравитация! Одна из фундаментальных сил. Она давит, она тянет, она хочет слепить всю материю в один комок. Причём, чем ближе две массы друг к другу, тем сильнее она тянет. Уменьшите расстояние между объектами в два раза, сила притяжения возрастёт в четыре. Что же не даёт всей материи схлопнуться в одну точку под действием гравитации? На первой линии обороны стоят электроны, формирующие «щит» вокруг атомного ядра. Это вступает в борьбу электромагнитное взаимодействие.

Мы знаем, что почти вся масса атомов сосредоточена в их ядрах, которые в десятки тысяч раз меньше диаметра атомов. Для сравнения, у самого лёгкого элемента – водорода радиус ядра составляет 0,875 фм (8,751 × 10⁻¹⁶ м) в ~60 тыс раз меньше радиуса всего атома 52,92 пм или 52,92 × 10⁻¹² м), у самого тяжёлого, встречающегося в природе – Урана радиус ядра 5,85× 10⁻¹⁵ м, что в ~26 тыс. раз меньше радиуса атома (156 пм или 156× 10⁻¹² м).

Чтобы лучше понять, насколько ядро атома маленькое, возьмите для масштаба горошину диаметром 5 мм, это будет как бы ядро, затем увеличьте её в 60 тыс. раз – получите шар диаметром в 300 метров – это будет атом. Электроны атома не дают сблизиться ядрам достаточно близко, чтобы ядра слиплись, так как отталкиваются друг от друга.

Но звёзды, звёзды они большие. Очень большие, и у них много массы. Огромное количество материи сдавливается до такой степени, что атомам остаётся становится всё меньше и меньше места, чтобы двигаться, они всё чаще соударяются друг с другом, давление растёт, а доступный объём уменьшается... то есть растёт температура. Когда мы говорим о температуре, на самом деле мы говорим о кинетической энергии частиц вещества. Рано или поздно, атомы начнут раздеваться терять свои электроны, если по-научному, то ионизироваться. Аналогия очень грубая и неправильная, но всё равно приведу пример – возьмите груз и привяжите к нему нитку. Теперь раскручивайте груз на нитке быстрее и быстрее (в данной аналогии – вы будете атомным ядром, а груз – электроном). Чем быстрее вы будете раскручивать, тем больше будет энергия груза. Рано или поздно нитка разорвётся и груз улетит – значит, вы ионизировались.

Много быстрых и голых атомных ядер без электронов называются плазмой. Ядра всё равно будут расталкиваться, так как они все положительно заряженные и требуется большая сила, чтобы можно было преодолеть этот барьер (кстати, он называется Кулоновский барьер). Но если хорошенько разогнать одно ядро в направлении другого, у него будет достаточно кинетической энергии, чтобы победить отталкивание и пасть в крепкие лапки сильного фундаментального взаимодейтствия (как оно работает, можно почитать в отдельном посте). Два (а бывает, и три) лёгких ядра сольются в экстазе, образуя более тяжёлое. Это называется термоядерный синтез, священный грааль человечества. Образовавшееся ядро будет легче, чем сумма масс врезавшихся друг в друга лёгких ядер, а разница вылетит в виде энергии (фотонов, электронов и нейтрино).

Так «горит» водород, превращаясь в гелий. Его запасы огромны, и большинству звёзд требуются многие миллиарды и даже десятки триллионов лет, чтобы сжечь его полностью, причём, вопреки интуиции, чем массивнее звезда, тем короче (но ярче!) окажется её жизненный путь. Малые звёзды, наоборот, живут очень и очень долго. Настолько долго, что мы до сих пор не знаем, что происходит со звёздами малого размера (с массой где-то в половину Солнца или меньше), так как ещё ни одна из них не умирала естественным образом.

Звёзды покрупнее (масса 0,4 – 3,4 Солнца) по мере израсходования запасов водорода имеют достаточную массу, чтобы гравитация сжала их ядро до такой степени, чтобы «поджечь» гелий, когда начнёт образовываться более тяжёлые элементы, вплоть до углерода. Этот процесс сопровождается выделением ещё большей температуры, и поток энергии от ядра становится настолько сильным, что, переборов гравитацию, начнёт раздувать внешние слои звезды. Звезда «пухнет» в размерах и превращается в красного гиганта. Давление на ядро уменьшается, реакции синтеза замедляются, тогда гравитация снова начинает сдавливать ядро, и они разгораются снова. Звезду «лихорадит», она постоянно меняет размеры, температуру, всё это сопровождается нарастающей потерей массы, которая превращается в звёздный ветер, богатый кислородом и углеродом.

«Горение» гелия продолжается около миллиарда лет. Если у звезды ещё остаётся масса, то «поджигаются» углерод и кислород, образовавшиеся на предыдущем этапе. Звезда ещё больше распухает, а потоки звёздного ветра усиливаются. Если масса всё ещё есть, «зажигается» неон, затем кремний, причём каждый следующий этап в разы короче предыдущего. Если «горение» водорода продолжается миллиарды лет, то когда «горит» кремний, счёт идёт даже не на дни, а на часы. Это последние часы перед смертью звезды, её последний вздох. Последними химическими элементами, которые синтезируются непосредственно в ходе термоядерных реакций является железо, никель и цинк, но до этой стадии могут дожить лишь тяжёлые звёзды, у более лёгких звёзд этот процесс может заканчиваться уже фтором.

Никель и цинк образуются, можно сказать, уже по инерции, ускоряя угасание звезды. Дело в том, что если при синтезе элементов легче железа энергии выделяется больше, чем тратится, то на синтез более тяжелых элементов энергии уже потратится больше, чем выделится. так что «гореть» внутри звезды становится уже нечему.

Всё время, пока в ядре звезды идут термоядерные реакции, давление исходящего от них излучения противостоит силе гравитации, старающейся сжать вещество как можно сильнее. Звезда находится в состоянии гидростатического равновесия. На последней стадии процесс становится очень интенсивным и быстрым. Что происходит дальше, целиком зависит от того, насколько тяжёлой была звезда.

Белый карлик

Гравитация сжимает оставшиеся атомы в ядре звезды настолько сильно, что электроны перестают «принадлежать» отдельным атомам. Сначала электроны заполняют все нижние орбитали, поскольку места на них больше нет – мы знаем (см. пост), что два электрона не могут находиться в одном квантовом состоянии из за принципа запрета Паули, электроны вынуждены занимать всё более и более высокие уровни.

Из-за того, что электроны не могут отдавать энергию путём перехода на забитые битком нижние этажи, материя, уже не представляет собой набор атомов, скорее, это набор положительно заряженных ядер, «плавающих» в море электронов. Такое состояние материи называется «вырожденный электронный газ».

Белый карлик (кстати, наше Солнце и большинство звёзд в наблюдаемой Вселенной превратятся именно в него) – это медленно остывающий остаток от небольшой звезды, состоящей из вырожденного электронного газа. Плотность его очень высока, чтобы получить такую плотность Солнце надо ужать до размеров нашей планеты. Звезда уже не производит энергию, но продолжает светиться, постепенно отдавая накопленную энергию, пока не остынет настолько, что превратится в чёрного карлика (хладный труп).

Электроны оказывают очень сильное сопротивление гравитационному сжатию из-за принципа запрета Паули, и, если масса звезды была недостаточной, то гравитация уравновешивается давлением вырожденного электронного газа... но если звезда оказывается тяжелее определённого предела (предел Чандрасекара), примерно в 1.44 масс Солнца, то гравитация пересиливает и буквально «вдавливает» электроны в протоны атомных ядер, превращая ядро в нейтронную звезду. Процесс называется обратный β-распад (англ.).

Нейтронная звезда

Но предшествует этому событию грандиознейший выброс материи в окружающее пространство.

Протоны и электроны под огромным давлением объединяются, в результате чего получается нейтрон. Нейтронная звезда, ВНЕЗАПНО, почти полностью состоит из нейтронов (за исключением внешней «шелухи» из обычного вещества). Коллапс звезды продолжается до колоссальной плотности. Высвободившаяся гравитационная потенциальная энергия выбрасывает очень горячее вещество, находящееся на внешних слоях звезды, в окружающее пространство с огромными скоростями (до 10% скорости света). В процессе звезда теряет очень много своей массы, зато в ходе данного взрывного процесса (кстати, это называется «взрывом сверхновой», не путать с «новой») происходит синтез почти всех остальных химических элементов, тяжелее железа.

Тут нужно сказать, что упомянутый всуе предел имени индийского астрофизика Субраманьяна Чандрасекара по массе звезды касается лишь массы её ядра. Для того, чтобы белый карлик превратился в нейтронную звезду, его масса (до взрыва) должна составлять примерно около 8 Солнечных масс. Масса в восемь Солнц оставляет «труп» массой всего в 1.4 массы Солнца, масса в 20 солнечных оставит ядро массой всего в три.

Диаметр нейтронной звезды, имеющей массу Солнца, составляет всего 10-20 км.

Средняя плотность её вещества составляет 2,8 × 10¹⁷ кг/м³. Такой материал называют «нейтронием». Это, в принципе, максимальная плотность, которую вообще может иметь материя, поэтому нейтроний так любим писателями-фантастами в качестве брони для космических кораблей. К сожалению, нейтроний может существовать только при давлении порядка сотен миллионов тонн на кв. см, и нет никакой возможности для его существования в нормальных условиях. Даже если представить себе гипотетически, что можно было бы достать образец подобного вещества из ядра нейтронной звезды, как только снизится окружающее давление, нейтроний тут же начнёт превращаться в обычную материю, при этом процесс будет сопровождаться многомегатонным «фейерверком».

Поскольку нейтрон тоже является фермионом (его спин равен ½) на него так же распространяется принцип запрета Паули, гласящий, что два фермиона не могут находиться в одном квантовом состоянии. Это значит, что хотя два нейтрона даже могут занимать физически одно и то же место, однако при этом иметь разнонаправленный спин, но больше нейтронов в эту область пространства поместить не удастся. Но и это препятствие не является непреодолимым. Если масса коллапсирующей звезды превышает определённый предел (на сей раз предел Оппенгеймера – Волкова, который на сегодняшний день определён в пределах 1,3 – 3 солнечных масс), последний барьер рушится и победившая всех гравитация в течение буквально секунд коллапсирует всю оставшуюся массу в безразмерную точку с бесконечной плотностью, называемой сингулярностью, а вокруг по радиусу Шварцшильда сформируется горизонт событий чёрной дыры.

Но такое происходит не так уж и часто, так как большинство звёзд в наблюдаемой вселенной имеют небольшую массу, и закончат свою жизнь как белые карлики.

Пульсары

Но вернёмся к нейтронной звезде. Нейтронные звёзды — один из немногих классов космических объектов, которые были теоретически предсказаны до открытия наблюдателями.

Впервые мысль о существовании звёзд с увеличенной плотностью ещё до открытия нейтрона, сделанного Чедвиком в начале февраля 1932 года, высказал известный советский учёный Лев Ландау. Так, в своей статье «О теории звёзд», написанной в феврале 1931 года и по неизвестным причинам запоздало опубликованной 29 февраля 1932 года (более чем через год), он пишет: «Мы ожидаем, что всё это [нарушение законов квантовой механики] должно проявляться, когда плотность материи станет столь большой, что атомные ядра придут в тесный контакт, образовав одно гигантское ядро».

Теоретические расчёты показали, что излучение нейтронной звезды слишком слабое, чтобы её можно было обнаружить при помощи астрономических инструментов того времени. Интерес к нейтронным звёздам усилился в 1960-х годах, когда начала развиваться рентгеновская астрономия, так как теория предсказывала, что максимум их теплового излучения приходится на область мягкого рентгена. Однако неожиданно они были открыты в радионаблюдениях. В 1967 году Джоселин Белл, аспирантка Э. Хьюиша, открыла объекты, излучающие регулярные импульсы радиоволн. Этот феномен был объяснён узкой направленностью радиолуча от быстро вращающегося объекта — своеобразный «космический радиомаяк». Но любая обычная звезда разрушилась бы при столь высокой скорости вращения. На роль таких маяков были пригодны только нейтронные звёзды. Объект PSR B1919+21 считается первой открытой нейтронной звездой.

На Земле излучение нейтронных звезд наблюдается в форме периодических сигналов. Астрономы выяснили, что у этого излучения естественное происхождение. Его строгая периодичность обеспечена особенной траекторией распространения. Дело в том, что нейтронная звезда излучает не во все стороны, как обычные звезды, а в форме узкого луча или веера. Вращаясь, нейтронная звезда, как маяк, просвечивает этим лучом космос. Поэтому радиоизлучение нейтронных звезд и наблюдается в виде ярко выраженных периодических пульсаций, оттого такие объекты и называются Пульсары.

Быстрое вращение пульсара объяснить проще. Все звёзды вращаются и, соответственно, имеют угловой момент, который сохраняется и при сильном уменьшении радиуса звезды. Уменьшение радиуса ведёт к пропорциональному увеличению скорости вращения.

Но что же является источником радиоизлучения нейтронной звезды? Ведь она состоит из нейтронов, а нейтроны электрически нейтральны и не могут участвовать ни в каком электромагнитном взаимодействии. Совершенно точно, не могут, но, как я уже сказал, на внешнем слое нейтронной звезды (примерно 1 км толщиной) давление не настолько сильное, чтобы материя деградировала, и в этом слое сохраняются протоны и электроны. Их вращение формирует магнитное поле, из полюсов которого и испускается электромагнитное излучение. За счёт потери этой энергии, вращение пульсара замедляется, и он «выключается». Это происходит достаточно быстро (примерно за 10-100 млн. лет), и большинство (99%) пульсаров, образовавшихся за время существования нашей Вселенной уже «выключились».

Нейтронные звёзды представляют большой интерес, так как по своему состоянию они являются самыми близкими к чёрным дырам объектами. Их гравитация настолько высока, что, если бы мы смотрели на них, то из-за релятивистского отклонения света мы бы видели больше половины их поверхности:

Многое в отношении нейтронных звёзд ещё предстоит узнать. Будем надеяться, что с появлением таких инструментов, как LIGO, и LISA мы ещё удивимся не одному открытию.