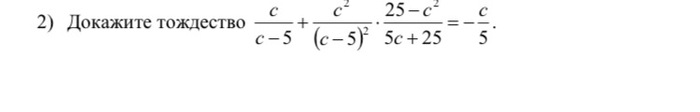ПОМОГИТЕЕЕЕ
Помогите доказать тождество
Олимпиадная математика
8 постов
•
13 подписчиков
Ответ на пост «Задачка для 6-го класса. Я не справился»1
Что-то все решали задачу в предположении, что шаров в каждом ящике поровну. Такое предположение мало того, что не дано в условии, но еще и несовместимо с даваемым ответом.
Но ответ многие получили правильный, хотя и неправильным способом.
Вот правильный способ.
Мы знаем, что белых шаров в каждом ящике столько же, сколько красных - во всех остальных.
Б1 = К2 + К3 + ... + К8
Б2 = К1 + К3 + ... + К8
...
Б8 = К1 + К2 + ... + К7
Мы не знаем, чему равны K1, К2 и так далее, но нам это и не нужно. Сколько всего белых шаров?
Б1 + Б2 + ... + Б8 = (К2 + К3 + ... + К8) + (К1 + К3 + ... + К8) + ... + (К1 + К2 + ... + К7)
Каждое К1, К2 и т.д. встречается в итоговой сумме семь раз. В принципе, это и без уравнений понятно.
То есть общее количество белых в семь раз больше общего количества красных: Б = 7К.
Аналогично С = 7Б.
Всего шаров С + Б + К = 49К + 7К + К = 57К. Условию задачи (сумма четная и меньше 130) соответствует только К = 2, общее количество 114.
Обратите внимание: равного количества шаров в разных ящиках в таком случае не будет. Ни 2 красных, ни 14 белых, ни 98 синих на 8 не делятся.
Варианта только два:
либо в одном ящике 2 красных и 14 синих шара, а в остальных семи ящиках по 2 белых и 12 синих,
либо в двух ящиках по 1 красному, 1 белому и 13 синих, а в остальных шести ящиках по 2 белых и 12 синих.
Показать полностью
Задачка для 6-го класса. Я не справился1
У меня получается 0 шаров в коробках. Помогите плиз решить.
Каждый год зимой происходят странности
Например, что-то пропадает. У одних важные вещи, у других новогоднее настроение. В этот раз — потерялись помощники Деда Мороза. Но есть хорошая новость: вы можете их найти! Вернее, помочь им найтись…
Напрягаем мозг друзья
Мир Вашему дому друзья и с наступающим.
Попалось интересное задание со школьной олимпиады. И пока мозги ещё не покрылись слоем оливье...может найдем решение?
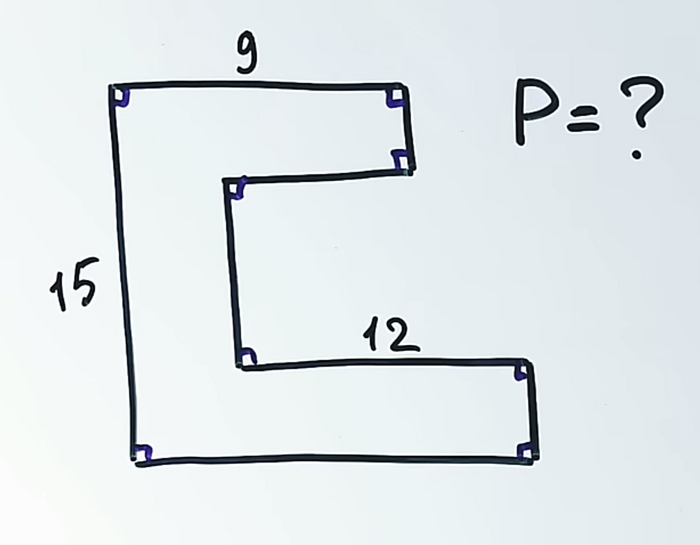
Нам известны длины трёх сторон многоугольника. Горизонтальные 9 и 12. Вертикальная 15. Также нам известно, что все углы прямые, т.е. 90°.
Нужно найти периметр фигуры.
Если вдруг интересно насколько Ваш мозг ещё шевелится, то прошу в ТГ канал. Правильное решение напишу там же.
Что важнее логика или математика? Задачка
1лицо берет в долг у 2 лица 100 у. е и теряет их. Тогда 1 лицо берет в долг у 3 лица 50 у. е. Из взятых в долг 50 у. е 1 лицо тратит 2 раза по 10 у. е. Оставшиеся 30 у. е 1 лицо возвращает 2 лицу. Вопрос- Сколько у. е 1 лицо осталось должно вернуть и куда пропали 10 у. е?
Математика+100-100+50-10-10-30=0
Логика. Долг 100+50 траты -20, возврат -30. Остаток общего долга 120 при затратах в 20 единиц кто украл 10 единиц? Церковная десятина? ( шутка)
Подготовка к олимпиадам по математике
Сам я являюсь призёром всероссийской олимпиады школьников по математике, хотя и учусь в 8-ом классе, а также обладателем второй степени олимпиады Эйлера, но всё это по нижней границе. Моё мнение о подготовке не может являться экспертным (по объективным причинам), лично я считаю, что получилось добиться такого результата в основном благодаря работе с хорошими преподавателями и удаче с задачами.
1) Важно участвовать в профильных сменах. Сейчас для любого региона существуют смены по математике в Сириусе, которые, как по мне являются лучшими. Летом лучше отбираться в Кировскую или Казанскую ЛМШ, которые так же считаются самого высокого уровня. Также, во многих регионах появились региональные центры, по работе с талантливой молодёжью, участие в профильных сменах, также, было бы весьма полезным.
2) У Московских математических кружков выкладываются все листочки. Архивы Кировской ЛМШ и смен Сириуса, также стараюсь прорешивать листочки. Приведенные выше источники считаю одними из самых сильных
3) В открытом доступе есть задачи олимпиады Эйлера, Всероса, Московских математических олимпиад и тд. полезно их прорешивать.
4) Хорошие книги - Ленинградские математические кружки (базовый уровень), Прасолов "Задачи по планиметрии", Виленкин "Комбинаторика", Алфутова Устинов "Алгебра и теория чисел".
5) Также есть много турниров математических боёв и игр: Лига Открытий, Лига Профессионалов, УТЮМы, Турнир памяти Колмагорова, ЮМТ и ТД. задачи которых полезно прореживать, ведь это фактически сборники разнобоёв.
Подготовка к олимпиадам
Всем добрый день!
Хотел поинтересоваться, как готовиться к всероссийской олимпиаде по информатике/экономике на уровень призёра.
Отправьте, пожалуйста, в комментарии полезные ссылки, книги, лекции.
Если кого-то интересует подготовка по математике, также могу об этом написать.