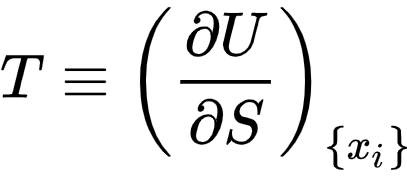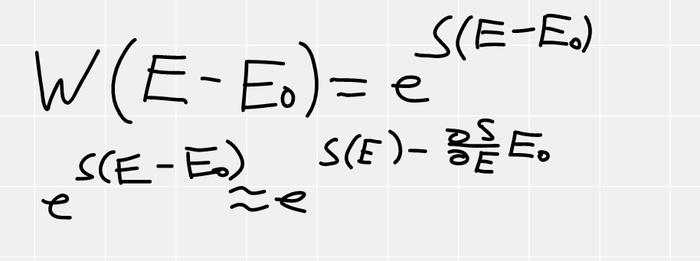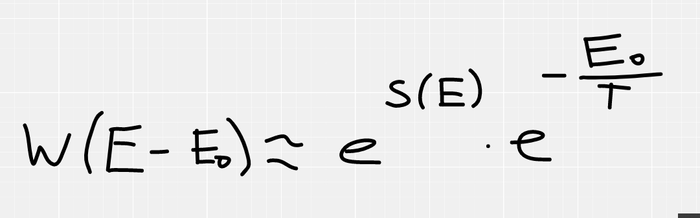us9000

Такие вещества называются эндоэдральные фуллерены. Это молекулы фуллеренов, в клетку которых заключены один или несколько атомов или молекул. Такие соединения обозначаются формулой Mm@Cn, где M — инкапсулированный атом или молекула.

Центральный атом в этих эндоэдральных комплексах расположен в центре клетки. В то время как другие атомные ловушки требуют сложного оборудования, например, лазерного охлаждения или магнитных ловушек , эндоэдральные фуллерены представляют собой атомную ловушку, которая стабильна при комнатной температуре и в течение сколь угодно долгого времени. Атомные или ионные ловушки представляют большой интерес, поскольку частицы присутствуют без (значительного) взаимодействия с окружающей средой, что позволяет исследовать уникальные квантово-механические явления.

Хоть эта запись и пугает всех, кто не знаком с курсом математического анализа, на человеческом языке, она означает "температура это скорость роста энергии при росте энтропии, при неизменном объеме, массе веществ, площади поверхностей и т.д."

Отлично, а что там в статистической физике? Ну условно, там та же формула, что и на картинке выше. Но лучше показать на простейшем примере.

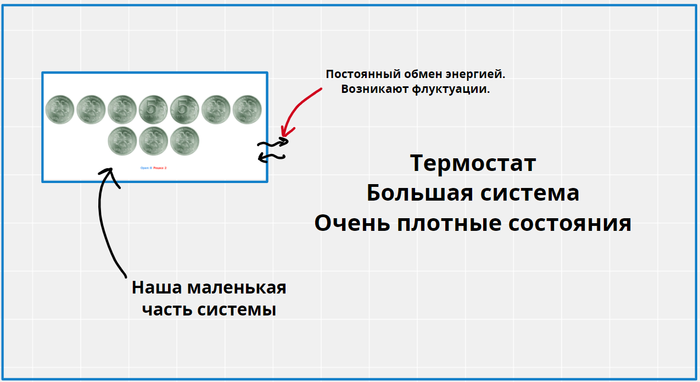
Для примера я возьму систему с десятью монетками. Давайте договоримся, что если монетка орлом вверх, то она имеет энергию 0, если решкой вверх, то энергия такой монетки будет у нас 1.

У системы на картинке энергия 2. У системы с десятью орлами, энергия будет 0. В прошлом посте я объяснял, как считают энтропию в статистике. Так что давайте посчитаем сколько микросостояний дает нам разную энергию.

E = 0 можно получить имея все монетки орлом вверх, это одно состояние, энтропия 0.

E = 1 можно получить имея одну решку, она может быть на первом, втором... и т.д. месте, микросостояний 10, энтропия k*ln10

E = 2 еще больше вариантов, их 45, а энтропия k*ln45

E = 3, вариантов 120, энтропия k*ln120

и т.д.

Реальные физические системы с таким простым набором состояний существуют, например система спинов в магнитном поле: типичная начинка квантового компьютера, атомы водорода в ЯМР спектрометре или они же в томографе.

У обычных больших тел (стакан воды, суп на плите, пробирка) квантовых состояний в невероятное количество раз больше, но с ростом энергии количество возможных вариантов аналогично растет, функцию E(S) можно вполне себе считать непрерывной. Для макрообъектов расстояние между уровнями энергии настолько мало, они так сгущаются, что измерить этот зазор невозможно даже в теории. Энтропию можно ввести и через классическую механику, рассматривая молекулы как шарики, правда там немного иначе она будет считаться, но ответ совпадает с квантовым рассмотрением.

Внимательные наверное уже заметили, что в определении температуры формула содержит производную, а в примере у меня дискретная функция, у которой нельзя посчитать производную. Именно так, понятие температуры в строгом смысле работает только для макроскопических объектов с кучей уровней, где мы не можем заметить, что функция E(S) дискретная. Для описания температуры объектов с малым количеством уровней, приходится сначала утверждать, что такая система находится в состоянии термического равновесия с термостатом (модельная среда, с конкретной температурой), но тогда наша система уже не имеет конкретную энергию, и имеет лишь вероятности находиться на том или ином уровне, ведь между маленькой системой и большим термостатом возникают флуктуации. Эти вероятности легко посчитать, пользуясь нашими формулами. Собственно для маленьких систем, температура уже будет иметь немного другой смысл, и быть скорее параметром, который описывает распределение вероятностей по уровням. О как!

Возьмем всё ту же систему с монетками, и попробуем выяснить как температура окружающей среды будет влиять на её энергию. Представим, что она находится в равновесии и контакте с какой-то другой системой, огромной по сравнению с ней, но при этом конечной.

Всё вместе мы представим изолированной системой с энергией E. Попробуем найти вероятность быть нашей системе в каком-нибудь состоянии с энергией E0.

У нас вся система, обладает каким-то набором микросостояний, пусть их W штук. Нам просто нужно найти сколько из них, подходят нам и поделить это число на общее количество.

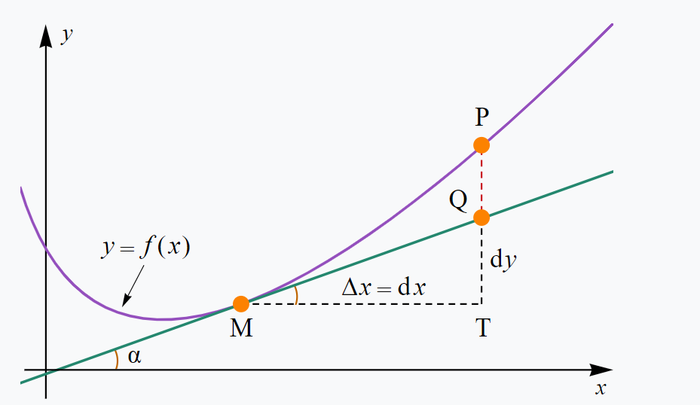
Если наша подсистема, в состоянии с энергией E0, то на термостат остается E-E0. Учитывая, что W=exp(S), получаем, что вероятность пропорциональна exp(S(E-E0)), но как это посчитать? Мы не зря посчитали, что термостат НАМНОГО больше чем наша подсистема, поэтому E0<<<E, а значит мы можем воспользоваться приближенным вычислением (в данном случае оно оказывается точным) с помощью производной. Рядом с точкой M, функция почти не отличается от своей касательной, в этом смысл дифференциала и производной.

Во всем выводе я убрал константу Больцмана, считайте, что я принял её единичкой, это не так важно.

В формуле появилась производная энтропии от энергии (что есть 1/T по определению из начала поста). И в конце концов мы получаем

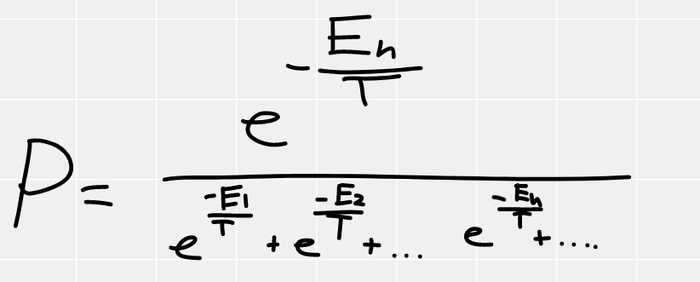
Вероятность должна быть пропорциональна W, при этом в сумме они все должны давать единичку, поэтому вероятность нашей маленькой системке находиться в n-ом состоянии (у которого энергия En), будет

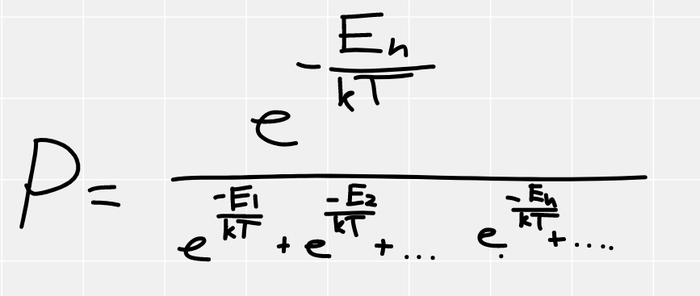
Если вернуть везде постоянную Больцмана, получится так

Снизу в формулах энергии всех остальных уровней. Очень симпатичная формула, называется распределением Гиббса. Из неё можно вывести распределения Максвелла, Больцмана и прочие прекрасные частные случаи. По ней видно, что если температура абсолютный ноль, то система находится в низшем состоянии с вероятностью 1, если же температура бесконечна, то система равновероятно может находиться во всех состояниях от низшего до наивысшего, что немного контринтуитивно (кажется, что бесконечная температура, это наивысшее состояние по энергии), но как видите это не так. Температура это сложный статистический параметр, а не просто энергия тела как нам кажется интуитивно.

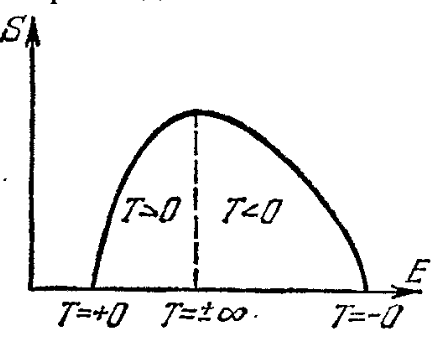
Еще один интересный вывод из такой формулы вытекает если наша система имеет конечное количество состояний (как наш пример с монетками имеет всего 1024 состояний, и 10 уровней), то возможно представить себе отрицательную температуру. Это состояние будет отвечать энергии системы даже большей чем, энергия системы при бесконечной температуре, ибо высшие уровни заселены чаще чем низшие (при бесконечной они поровну все заселены). Мы можем создать искусственно такие состояния в реальности, ведь системы с ограниченным количеством уровней существуют, а способы "перевернуть заселенность" существуют.

Но откуда же у нас всех берется знание, что температура отвечает за скорость молекул? А дело в том, что если мы применим распределение Гиббса к идеальному газу, то средняя кинетическая энергия молекулы будет 3/2kT, об этом нам рассказывают в школе сразу в готовом виде (исторически температуру с этого случая вводили и в науке), и на этом же эту тему заканчивают, отсюда и остается подобный обрубок понимания довольно сложного понятия температуры.

Учитывая, что статистическая физика и термодинамика стоят на очень простых принципах из математики, выходит довольно любопытная ситуация. Дело в том, что и общая теория относительности, и квантовая механика отлично стыкуются с термодинамикой. Но как мы знаем, между собой ОТО и КМ очень плохо стыкуются, и квантовую теорию гравитации до сих пор не разработали. Так же мы знаем, что внутренности и поверхности черных дыр, обладая страшной кривизной пространства-времени, должны описываться той самой пока несуществующей квантовой теорией гравитации, но мы точно понимаем, что эта теория должна тоже хорошо стыковаться с термодинамикой. Изучение термодинамики черных дыр сразу показало, что они должны обладать температурой и излучать, позже Хокинг более подробно описал это излучение, которое назвали в его честь, но это уже совсем другая история.

Закончу пост цитатой Эйнштейна:

«Теория производит тем большее впечатление, чем проще ее предпосылки, чем разнообразнее предметы, которые она связывает, и чем шире область ее применения. Отсюда глубокое впечатление, которое произвела на меня классическая термодинамика. Это единственная теория общего содержания, относительно которой я убежден, что в рамках применимости ее основных понятий она никогда не будет опровергнута» 

Эйнштейн А. Собр. науч. трудов М.: Наука, 1967. Т. 4. с. 270

Получается, что чашка вполне себе может обратно залететь на стол и собраться. Но почему этого не происходит? Во всем виноват единственный физический закон, которому не плевать на стрелу времени, это второй закон термодинамики, закон неубывания энтропии.

Энтропия, физическая величина, введенная Клаузиусом (1865), является аддитивной функцией состояния. Т.е. у любой системы помимо массы, энергии, объема и т.д. мы можем добавить энтропию как еще одну величину. Если система состоит из двух меньших, то общая энтропия равна сумма энтропий этих двух систем (собственно как масса, энергия или объем).

Но что это такое? Мы все понимаем интуитивно что такое энергия, что такое масса, что такое объем, и почему их можно складывать. Мы даже интуитивно можем понять что такое температура и давление, но что такое энтропия? Просто число? Математический трюк для решений задачек по термодинамике? У неё есть физический смысл? Почему, если законы физики можно отражать во времени обратно, она растет? Ведь любая система состоит из частиц, которые вполне себе подчиняются этим законам? В 1877 году Людвиг Больцам нашел ответ.

Если следовать Больцману и Планку, статистическая энтропия системы равна k*ln(W). Где k - константа, ln - натуральный логарифм, W - количество микросостояний, описывающих данное макросостояние системы.

Если после прочтения последней фразы у вас вот такое лицо

не удивляйтесь. Оно обычно такое у всех после прочтения определения W в учебнике. Попробую объяснить понятным языком. Сразу скажу, что понятие "мера хаоса", это довольно притянутая за уши противоречивая штука, поэтому я сразу откидываю нафиг все эти попсовые "меры хаоса". Проще всего объяснить статистический смысл энтропии через меру нашего незнания.

Начну я вообще внезапно с другой стороны. Начну я с лотерейного билетика. Да, обычный лотерейный билетик. Представим, что на нем есть 10 неизвестных цифр, скрытых от нас.

Если мы не стерли защитный слой, какое наше незнание? Ну, под ним может оказаться

10^10=10 000 000 000 вариантов. Если же мы сотрем защитный слой, наше незнание исчезнет, и мы будем видеть конкретный набор из 10-ти цифр. Вариант останется только один.

Если попробовать посчитать энтропию по формуле, получим в первом случае

Во втором случае ноль, ибо логарифм единицы это ноль. Вы спросите, а зачем в формуле константа и логарифм? Неужели нельзя было просто сказать "раз вариантов 10^10, то пусть энтропия будет равна количеству вариантов"? Можно, но мы же пытаемся привязать энтропию из статистики к энтропии которую ввел Клаузиус. Поэтому константа там нужна для связи с энергией, а логарифм обеспечивает тот факт, что энтропию системы можно получить сложением энтропии отдельных независимых кусочков.

Смотрите сами, если мы возьмем два билета из разных лотерей, и спросим, а какая энтропия скрытых номеров? То если у первого билета X вариантов, у второго Y вариантов, то у двух билетов вместе будет X*Y вариантов. Но по свойству логарифмов ln(XY)=ln(X)+ln(Y), поэтому энтропия двух билетов будет равна сумме энтропий каждого (прям как у Клаузиуса).

Для реальных систем всё точно так же. Возьмем что-то простое, например один моль аргона (40 грамм), при температуре в 20 градусов и давлении в одну атмосферу, эти параметры (температура, давление и количество газа) полностью описывают состояние этого газа. Зная их, мы можем найти и плотность, энергию, объем, среднюю скорость молекул. В общем, зная три параметра, мы можем найти все остальные макроскопические параметры. Для нас, две порции аргона абсолютно одинаковые, если имеют одинаковую температуру, объем и давление.

Но можем ли мы получить значения скоростей и координат всех атомов аргона? Конечно же нет. Чтобы описать все скорости и координаты у одного моля аргона, нам понадобится 3.612*10^24 значений скоростей и координат. А мы знаем только три, и те являются что-то типа усреднения. Это как если бы вас попросили, по средней зарплате в регионе, узнать зарплату каждого человека. Это просто невозможно.

Большая ли энтропия у такой системы? В случае с десятью цифрами у нас рождалось 10^10 вариантов, тут же будет такое число, которое даже записать в степенном виде довольно сложно, нужно будет писать степень в степени. Мы очень много не знаем.

Если что, энтропия одного моля аргона при температуре 20 градусов где-то 150 Дж/К

Если посчитать W в обратную сторону, выйдет e^(1.12048793*10^25), да-да, степень в степени, это невообразимое число.

Получается, что второй закон термодинамики утверждает, что наше незнание о микросостоянии системы должно расти и принимать максимальное значение, где мы знаем только макроскопические параметры, потеряв все остальные знания о микросостоянии. Но как? Почему это происходит? Законы физики позволяют нам просчитать всё наперед, если мы знаем начальные условия, второй закон даже требует изолированности системы, что даже сильнее связывает возможность куда-то потерять информацию. Да и сами законы, по которым частицы передвигаются в системе, подчиняются симметричным по времени законам (о чём я писал в начале поста). У подобного парадокса есть несколько объяснений:

2) Внешнее влияние всегда есть. Идеально изолированных систем не существует.

"Хаос" в физике и математике сильно отличается по значению от бытового контекста слова "хаос". В точных науках, хаотическими системами называют такие, которые при малейшем изменении начальных условий, будут давать кардинальные отличия через какое-то время.

Летящий в космическом вакууме камень, не является хаотической системой, хотя влияние начальных условий всё-равно существует, если вы поменяете его начальную скорость на 0.0001 м/с, то через год, такой камень будет уже на 3153 метра отходить от его изначальной траектории. Хаотические системы накапливают изменения во много раз быстрее, так быстро, что многие хаотические системы выглядят для нас случайными. Типичная классическая хаотическая система это атмосфера. Даже упростив уравнения модельной атмосферы до минимума, она будет оставаться хаотичной. Первым это подметил Лоренц, как раз пытаясь немного разобраться с погодой. В массовой культуре этот интересный математический вывод известен как эффект бабочки. А в повседневной жизни нам приходится мириться с тем, что прогноз погоды часто врёт, метеорологи просто математически не имеют возможности точно предсказывать погоду через неделю, а курсы валют и акций порой делают такие взлеты и падения, что все аналитики хватаются за головы. Особо сложной хаотической системой является общество.

Из простых хаотичных систем, самая понятная для представления это двойной маятник. Вот моя любимая иллюстрация насколько для него важны начальные условия:

На видео симуляция тысячи двойных маятников, которые отличаются в начальных условиях на самые мизерные доли градуса.

Молекулы газа в банке, если описывать их классической механикой, тоже являются хаотической системой.

Поэтому для предсказания будущего положения частиц, нам необходимо однозначно знать начальные условия, и иметь идеально изолированную систему.

Ни одно из этих условий невозможно выполнить: принцип Гейзенберга из квантовой механики запрещает нам знать однозначно точно как положения так и импульсы частиц, а идеально изолированных систем в принципе не существует, и поэтому помехи рано или поздно подмешают нам ошибку. Поэтому наше незнание, а следовательно и энтропия будут расти, пока не упрутся в максимальное значение, равное термодинамической энтропии.

Если же пойти в лоб и сказать "это всё потому, что ты считаешь молекулы газа шариками, бери давай считай уравнениями квантовой механики", то мало что поменяется. Все аргументы останутся в силе, хоть и немного преобразуются. Плюс добавится еще одна штука, добавляющая нам незнания в систему. А именно эффект наблюдателя.

Если наша система находилась в состоянии квантовой суперпозиции, то при измерении мы получим лишь один результат из многих возможных. Это однозначное нарушение симметрии по отношению ко времени играет на руку второму закону термодинамики. Ведь под наблюдением понимается не только наш осознанный способ измерить что-то, но и банальное взаимодействие системы с окружающей средой. Само явление, утрачивания квантовой системой информации о состоянии, называют декогеренцией.

Декогеренция является одним из самых существенных технических препятствий на пути создания квантовых компьютеров. Для борьбы с декогеренцией разрабатываются, с одной стороны, различные методы изоляции квантовой системы, включая использование крайне низких температур и высокого вакуума, а с другой — введение в квантовые вычисления кодов, устойчивых к ошибкам, связанным с декогеренцией (обычно в таких схемах состояние логического кубита кодируется состоянием нескольких связанных физических кубитов). Квантовым компьютерам приходится сражаться с самой энтропией, чтобы просто хоть как-то работать.

Что в итоге? В итоге получается, что достоверно предсказать будущее мы можем только для ограниченного количества систем, в которых мы очень точно можем узнать начальное состояние, а внешние воздействия минимальны по отношению к процессам, происходящим в этих системах. Например, поведение планет можно просчитать на достаточно длительный период времени, а вот предсказать курс рубля или погоду на неделю вперед достоверно не получится.

Второй закон термодинамики неумолим, и не работает только для действительно изолированных нехаотических систем, в которых погрешность определения начального состояния никак не растет. Таких систем просто не существует. Из-за него железные изделия ржавеют, а молоко размешивается в кофе и никак не в обратную сторону, а мы стареем и наша память портится. Процессы, в которых потеря информации о микросостояниях сильно влияет на макросостояние, для нас выглядят необратимыми и всегда подсказывают нам, когда видео запускают в обратную сторону. Причем тот факт, что энтропия растет, но сами уравнения симметричны относительно времени, создают дикую вещь для потенциальной машины времени, она просто не будет работать, так как с точки зрения квантовой механики, если у будущего есть несколько вероятных исходов, значит и у прошлого есть несколько вероятных вариантов. Попробовав передвигаться в обратную сторону, второй закон будет вести вас по таким вариантам прошлых моментов, что вам просто покажется, что ничего не изменилось, а вселенная просто отразилась в зеркале.

Но не всё так плохо, и тут я добавлю оптимизма, полный хаос на микроуровне не всегда означает хаос для макроскопических параметров. Подавляющая часть этих необратимых процессов идет предсказуемо в макромасштабе. Размешивание газа в комнате необратимо, но всё-равно это будет происходить каждый раз с одинаковой скоростью и это можно даже рассчитать. И со старением всё тоже оптимистично, мы открытые системы, а значит теоретически никакого запрета иметь бессмертное тело нет. Но конечно же его придется подлечивать от старения время от времени, и воспоминания будут потихоньку портиться.

В этом посте я хотел добавить еще довольно большую часть, которая бы рассказала, как именно статистика, энтропия, количество микросостояний связаны с энергией тела и понятием температуры, т.е. большая часть людей на самом деле не знает, какой смысл несет температура в разных разделах физики, а в школе отделываются условным "мера скорости движения молекул", что является довольно неточным смыслом. Но тогда пост стал бы раза в два больше, а он и так утомительный. Так что может быть когда-нибудь потом.