
Энергетика
3 поста

3 поста

7 постов

9 постов

2 поста

11 постов
12 постов
5 постов
Продолжение. Часть 1, часть 2.
В первой части своего повествования, я упомянул как аксиому тот факт, что скорость света постоянна и не зависит от системы отсчёта, однако, не рассказал, зачем вообще нашей вселенной понадобилось ограничивать максимальную скорость передвижения. Данный пост я хочу посвятить исключительно ответу на вопрос
ЗАЧЕМ ВСЕЛЕННОЙ СКОРОСТЬ СВЕТА И ПОЧЕМУ СВЕТ ЗДЕСЬ НИ ПРИ ЧЁМ?
Имеет ли скорость света какое-либо отношение собственно к свету? Что же делает скорость света такой «специальной», почему мы наблюдаем такой «Вселенский» заговор, препятствующий всем фотонам (да что там фотонам – чему угодно!) перемещаться быстрее, чем предельные 299 тыс. км/с?
Ответ — данное утверждение ложно. Вернее оно перевёрнуто с ног на голову. Вселенная не устроена так, чтобы поддерживать скорость света постоянной, в действительности пространству-времени наплевать на свет, оно и сейчас расширяется быстрее скорости света и при этом ещё и продолжает ускоряться. Вселенское ограничение скорости имеет более глубокие корни.
В предыдущем посте я уже затронул причинность при рассказе о пространственно-временных интервалах. Причинно-следственные связи — это единственное, о чём могут договориться любые наблюдатели, находящиеся в любой системе отсчёта.
Но почему у причинности имеется максимальная скорость? И почему эта скорость случайно совпадает со скоростью света в вакууме?
Давайте разбираться, и начнём мы издалека, с 1632 года, когда Галилео Галилей предстал перед судом Святой Инквизиции за его поддержку в своей книге идей Коперника о гелиоцентрической системе мироустройства. Однако, кроме всего прочего, в своей книге Галилей так же упомянул «принцип относительности», который его словами звучал примерно так:
Галилео заявлял, что не только нет никакого особенного места, но и нет никакой особенной скорости, которая могла бы повлиять на исход «механического эксперимента» в системе, которая движется прямолинейно и без ускорения. Это одно из великих предвидений Галилея было позднее кодифицировано другим гигантом — Исааком Ньютоном в своих «законах».
Перенесёмся на 200 лет позднее для того, чтобы встретить ещё одного героя нашего рассказа – Джеймса Кларка Максвелла, который умудрился вплести эти законы в 4 уравнения, элегантно описывающие весь феномен электромагнетизма.
К концу 19 века у нас были законы Ньютона, уравнения Максвелла, ещё несколько теорий, и общее ощущение того, что физика закончилась и вселенная познана... кроме двух маленьких проблемок — первые намёки на квантовую природу Вселенной и небольшую сумятицу, которые уравнения Максвелла внесли в Галилееву относительность. Вообще, и Ньютонова механика негласно опиралась на предположение, что скорость света бесконечно велика, а если бы это было действительно так, то это повлекло бы весьма серьёзные осложнения, однако, давайте разберёмся с уравнениями Максвелла, вот они:
Эти уравнения настолько значимы, что отлиты в бронзе на его памятнике. Не пугайтесь, примерный смысл этих уравнений выражается следующим образом:
1. Электрический заряд является источником магнитной индукции (теорема Гаусса).
2. Магнитный заряд отсутствует (теорема Гаусса для магнитной индукции)
3. Изменение магнитной индукции порождает вихревое электрическое поле (закон индукции Фарадея)
4. Электрический ток и изменение электрической индукции порождают вихревое магнитное поле (закон Ампера - Максвелла).
Тот перевёрнутый треугольник называется "набла" - это просто индикатор особой операции, чуть сложнее, чем операторы + или —.
Но будем проще. Позовём наших друзей, Алису и Бориса, которые путешествуют на железнодорожной платформе. При этом Алиса ещё катается на скейте... и она электрическая, нам ведь нужно что-то электрически-заряженное, чтобы генерировать магнитное поле. Выглядит это как-то так:
Перемещаясь по платформе, Алиса генерирует магнитное поле, и мы, зная уравнения Максвелла, можем посчитать силу данного поля, зная полную скорость Алисы (v1 + v2). Мы так же можем прямо измерить эту силу при помощи физического эксперимента.
Борис — кот учёный и тоже умеет считать. Наблюдая за перемещениями Алисы со скоростью v1 он так же посчитает силу магнитного поля... и что-то не сходится. Очевидно же, что сила магнитного поля, которое генерирует Алиса, одна и та же. Мы измеряем не само поле, а его эффект — силу Лоренца — зависимый от скорости баланс между электрическим и магнитными полями. Оба поля работа работают, чтобы создать эту силу (полная сила электромагнитного поля на движущийся со скоростью v заряд q, в которую вносит свой вклад как электрическое Е, так и магнитное B поля:
F = q(E + [v × B])
Причём, сила эта не зависит от системы отсчёта. Это наводит нас на мысль о том, что электромагнитная сила каким-то образом связывает скорость и пространство-время. Как же нам выявить эту связь? Борису и нам нужна какое-нибудь волшебное преобразование, позволяющее переводить уравнения Максвелла из одной системы отсчёта в другую.
Таким примером могло бы служить Галилеево преобразование, которое просто говорит о том, что скорости складываются, а пространство и время не зависят от скорости. То же самое преобразование использует Ньютоновская механика, и мы только что применили их для преобразования уравнений Максвелла к скорости Алисы.
x' = x – vt
Но внезапно оказалось, что к уравнениям Максвелла нельзя применить Галилеево преобразование таким образом, чтобы они выдавали непротиворечивые результаты, иными словами они НЕ ИНВАРИАНТНЫ!
Вроде бы они и выдавали правильные значения для низких скоростей, но приводили в полный хаос векторные составляющие полей, а для высоких скоростей эти значения... нет, просто забудьте о высоких скоростях! Физика совсем поломалась!
После преобразований, линии напряжённости магнитного поля будут выглядеть как-то так:
Так что же, Максвелл был неправ? Нет, как выяснилось, неправ был Галилей.
Преобразования, на которых работала Ньютоновская механика, были неправильными. Единственные работающие преобразования, были Лоренцевы (о них я рассказывал в первой части), но до сего момента они были чуть больше, чем некая математическая абстракция для преобразования поворота в четырёхмерном пространстве (к слову, к современному виду их привёл французский математик Анри Пуанкаре за 5 лет до Эйнштейна в 1900 года, который об этой работе не знал и сделал то же самое лишь в 1905).
Лоренцевы преобразования были известны задолго до Эйнштейна. Кому интересно узнать больше, на Википедии есть хорошая статья про то, как их можно вывести самостоятельно в домашних условиях.
Вкратце, история сводится к следующим логическим выкладкам:
Давайте честно признаем, что сложение скоростей (v1 + v2) не работает! Необходимо другое преобразование!
Законы физики работают неизменно, вне зависимости от положения, ориентации или скорости. Нам абсолютно не важно, где находится Алиса, в каком направлении, и с какой скоростью она движется. Это должно быть так — Земля вертится вокруг своей оси, вращается вокруг Солнца, Солнце вращается вокруг центра Млечного пути, наше положение, ориентация и скорость меняются кардинальным образом, в зависимости от нашей точки зрения, но наши физические эксперименты выдают одни и те же результаты, несмотря на это.
Теперь давайте сделаем ещё одно смелое предположение — что Вселенная устроена логично!
Добавим так же требование, что нам постоянно необходимо делать преобразования между разными системами отсчёта туда и обратно и получать непротиворечивые результаты — мы должны иметь возможность пройти путь преобразований при переходе из в системы отсчёта Алисы к системе отсчёта Бориса, затем – в нашу систему отсчёта, откуда мы их наблюдаем, а затем повторить весь путь назад к Алисе и получить те же результаты, с которых мы начали, при этом изменяя лишь один параметр — скорость.
И наконец, добавим ко всему этому щепотку алгебры — получим преобразования Лоренца. Единственное преобразование, которое отвечает всем нашим требованиям!
Эйнштейн заподозрил, что поскольку данные преобразования столь хорошо справляются сзадачей, возможно, они описывают некие фундаментальные законы самой природы пространства-времени, природы нашей реальности.
Однако, в формуле преобразования Лоренца присутствует некая константа c, значение которой нам неизвестно.
Физический смысл этой константы – вселенский скоростной предел. Почему? Потому что без неё константы, преобразования Лоренца бы попросту не работали, данная константа — необходимый элемент формулы преобразования, без которого обойтись невозможно. Преобразования Галилея — это лишь частный случай преобразований Лоренца, гдс c = ∞. И действительно, с точки зрения симметрии и относительности, константа c действительно могла бы быть бесконечной.
При помощи преобразований Лоренца, наконец, позволили получить инвариантные версии уравнений Максвелла (согласованное значение для магнитного поля Алисы, вне зависимости от системы отсчёта: нашей, Бориса, либо её собственной), без них, мы бы не смоли дать описания законам электромагнетизма — это стало ещё одним подтверждением того, что данные преобразования корректно описывают окружающую нас действительность.
Однако, не любое значение константы с нам подойдёт. Данное значение должно быть комбинацией значений фундаментальных констант в уравнениях Максвелла, иными словами, для того, чтобы электрические законы и законы магнетизма работали, нам так же необходимо ограничение — совершенно определённое значение константы c в формуле преобразования Лоренца.
Так что же это за значение? Да можно просто найти его комбинируя результаты физических экспериментов с электромагнитными полями, а затем — применять к этим значениям преобразования Лоренца туда и обратно с разными значениями с. Когда после преобразования из одной системы отсчёта в другую и обратно результаты совпадут с исходными, это и будет требуемым нам значением. Но подождите... ВНЕЗАПНО оказывается, что значение, которое мы нашли, в точности совпадает с измеренной скоростью распространения электромагнитных волн — скоростью света.
Ещё со времён Ньютона мы знаем, что масса обременяет движение, если же у чего-либо отсутствует масса, то нет и никаких препятствий двигаться настолько быстро, насколько это вообще возможно. Фотоны, гравитационные волны, глюоны — всё, что не имеет массы движется в нашей Вселенной с максимально-возможной скоростью. Соответственно, и для передачи информации (взаимодействия) между двумя уголками Вселенной, максимальной скоростью будет являться скорость распространения электромагнитных волн в вакууме.
Иными словами, скорость света, это максимальная скорость распространения причинно-следственных связей — скорость причинности.
Взгляните на рисунок — это трёхмерное представление уже знакомой нам диаграммы Минковского. К нашему настоящему моменту (красная стрелка показывает наблюдателя) из прошлого сужается воронка — наш «световой конус прошлого». На наше текущее настоящее может повлиять только событие, которое попадает в рамки данного конуса — этот конус — наш «горизонт событий». В будущее воронка расходится и включает в себя все события, на которые мы в состоянии повлиять из настоящего момента. Если событие находится за пределами нашего светового конуса, то причинно-следственной связи между такими событиями быть не может.
Интерпретация Эйнштейном ФИЗИЧЕСКОГО СМЫСЛА преобразований Лоренца и дала нам Специальную Теорию Относительности, установив фундаментальную связь между пространством и временем.
Так что бы было, если бы не было этого Вселенского ограничения скорости? Если мы оставим значение c = ∞ (сейчас речь о константе c в преобразованиях, а не о скорости света), то не было бы и массы, так как на создание какой-либо массы потребовалось бы бесконечное количество энергии (E = mc²), во вселенной существовали бы только безмассовые частицы, перемещающиеся на бесконечной скорости.
Существование самого пространства-времени было бы невозможным – с бесконечным замедлением времени и сокращением расстояний до нуля, между событиями отсутствовали бы причинно-следственные связи (вернее, любое бесконечно-удалённое и бесконечно-давнее событие могло бы повлиять на любое событие в бесконечном будущем и наоборот), был бы вселенский хаос — безвременной танец безмассовых частиц в вечном «здесь и сейчас».
Разумеется, мы не могли бы существовать в подобном парадоксе. Для возникновения нашей Вселенной, ей просто необходимо было ограничить максимальную скорость причинно-следственных связей, иначе она попросту не могла бы возникнуть и существовать .
В следующей части мы поговорим об эквивалентности массы и энергии и об истинном смысле формулы E = mc².
Первая часть моей релятивисткой поэмы была посвящена больше инструментам, которые должны помочь нам разобраться с некоторыми аспектами специальной теории относительности (СТО) – диаграммами Минковского и преобразованиями Лоренца. В этой части мы начнём использовать эти инструменты, чтобы разбирать конкретные кажущиеся парадоксы.
Итак, когда мы хотим перемеситься из неподвижной системы отчёта в подвижную или обратно, на помощь нам приходят преобразования Лоренца:
Одним из важных свойств данных преобразований является то, что события, которые в одной системе отсчёта происходили в одно и то же время, вовсе не обязательно будут одновременными в движущейся системе. Это влечёт за собой вывод – события, которые неподвижному наблюдателю кажутся одновременными, не будут являться таковыми для движущегося наблюдателя —
ОДНОВРЕМЕННОСТЬ ОТНОСИТЕЛЬНА!
Иными словами наблюдатели, один из которых неподвижен, а второй движется, никогда не смогут договориться об одновременности каких-либо событий.
На диаграмме внизу видно, как три события A, B и C, которые происходят одновременно для неподвижного наблюдателя (имеют одну и ту же вертикальную временную координату), для движущихся наблюдателей, эти события уже не одновременны, более того, наблюдатети, движущиеся с разной скоростью будут спорить друг с другом так же и порядке их наступления:
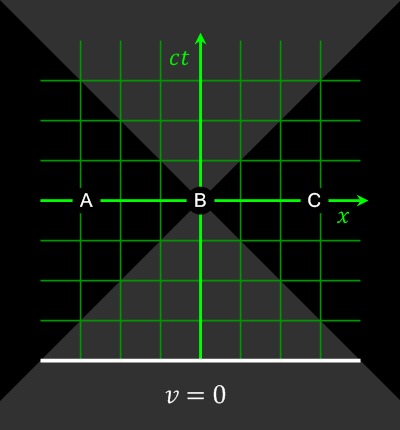
Если мы приглядимся к формуле Лоренцева преобразования для скорости, мы увидим, что новая временная координата зависит и от скорости и от первоначального положения события в пространстве. Из-за того, что в знаменателе стоит скорость света в квадрате — астрономическое число (89 875 517 873 681,764 км/с – восемьдесят девять триллионов километров в секунду), при малых скоростях данная часть формулы практически всегда равна 0, однако, при увеличении скорости и расстояния до события до значений, сопоставимых со скоростью света растёт и разница в восприятии временной координаты данного события.
Одними из наиболее удивительных свойств преобразований Лоренца являются релятивистское замедление времени и Лоренцево сокращение. Оба эффекта являются, так или иначе, следствием свойства относительности одновременности.
Давайте разберёмся для начала с замедлением времени.
Предположим, Алиса движется на 33% скорости света, и у неё есть секундомер, которым она отмеряет каждую секунду своего путешествия. Борис остаётся неподвижным, и у него тоже есть секундомер. Алиса смотрит в телескоп на секундомер Бориса, сравнивает его показания со своим секундомером и выясняет, что у Бориса каждая секунда длится примерно на 6% дольше. Эту картину мы наблюдаем на следующей диаграмме, которая показывает, каким мир видит Алиса.
Но тут Борис тоже решил взглянуть через телескоп на секундомер Алисы и сравнить показания. Внезапно оказывается, что это у Алисы часы идут медленнее, чем у него, что мы видим на следующей диаграмме (скорость указана -0,33с).
На самом деле, разбираться, кто из них прав, смысла большого нет, так как оба наших героя забывают об относительности одновременности. Алиса считает, что каждую секунду Бориса, на её часах проходит 1,06 с, она предполагает, что её часы синхронизированы с часами Бориса, однако в её системе отсчёта, это уже не так. Если два секундомера разделяет расстояние L, каждый из наблюдателей будет видеть на часах другого задержку в v * L/c^2 секунд.
Чтобы ещё более наглядно представить себе суть явления замедления времени, давайте сконструируем особые часы, состоящие из двух зеркал, расположенных друг напротив друга, а между ними пульсирует луч света, отражаясь поочерёдно от каждого зеркала, отсчитывая, таким образом, равные интервалы времени. Если мы сядем в космический корабль, разгонимся и будем смотреть на это устройство, то будем наблюдать нечто подобное:

Если же мы отправим данное устройство в полёт, а сами останемся на Земле, то картина, которую мы будем наблюдать, будет уже другой:

Очевидно, что теперь луч света проходит большее расстояние от зеркала до зеркала и, соответственно, длительность каждого импульса будет дольше.
Лоренцево сокращение
Для начала суть: длины движущегося по отношению к нам объекта будут нам казаться короче, чем они есть.
Предположим, у нас есть движущийся стержень определённой длины. Мы измеряем стержень, двигаясь вместе с ним, в его собственной системе отсчёта (на диаграмме – отрезок OB), затем повторяем измерение из неподвижной системы отсчёта (получаем отрезок OC). Как видим из эксперимента, длина движущегося стержня в неподвижной системе отсчёта будет короче.
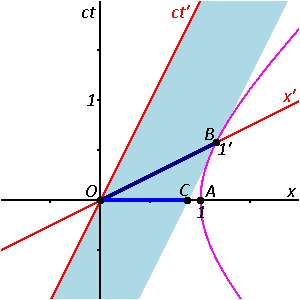
Невольно может возникнуть вопрос: а какая же длина истинна? Правильного ответа на данный вопрос не существует. Вернее, оба варианта – правильные. Длины в нашем мире относительны, поэтому ответ на данный вопрос требует уточнения – в какой системе отсчёта?
Корни данный феномен берёт всё так же – из относительности одновременности. Сам факт измерения длины предполагает вычисления разности пространственных координат начала и конца стержня, причём эти координаты должны быть взяты ОДНОВРЕМЕННО. Однако, как мы уже поняли, в нашем мире два события, произошедшие одновременно для одного наблюдателя, вовсе не будут одновременными для другого.
А что же сам свет? Давайте подставим в формулы преобразований Лоренца скорость света. Строго говоря, нам это не удастся из-за коэффициента гамма:
Как видно, если мы подставим в качестве v скорость света, весь знаменатель обратится в ноль, а на ноль делить нельзя иногда можно.
С математической точки зрения, данное выражение будет лишено смысла, однако физически сам свет (и любые безмассовые частицы) перемещается в вакууме, не испытывая течения времени вообще. Более того, для фотона света так же не существует и расстояний, так как любое расстояние для него равно нулю. Для фотона света существует только постоянное здесь и сейчас.
Сложение скоростей
Предположим, у нас есть пистолет, который стреляет удивительно-быстрыми пулями на скорости 60% световой. Если мы построим диаграмму подобного выстрела, то она будет выглядеть следующим образом:
Предположим теперь, что мы произвели выстрел из того же пистолета, но при этом мы сами уже двигались на скорости 50% световой. Классическая механика подсказывает нам, что для нахождения скорости пули относительно неподвижного наблюдателя, необходимо сложить нашу скорость 0,5 с и скорость пули 0,6 с, что в сумме даст 110% скорости света.
Однако, в действительности сложение скоростей работает, разумеется не так, в чём легко убедиться, если мы сдвинем ползунок скорости до 0,5 с:
Как мы видим, пуля по-прежнему летит быстро, но по-прежнему не превышает скорость света (жёлтая линия, проходящая под 45° к основным осям). В релятивистской механике сложение скоростей так же зависит от скорости света и считается по формуле:
где v1 и v2 – скорости складываемых объектов. Так, скорость нашей пули в движущейся системе отсчёта будет примерно равна (0,5 + 0,6) / (1 + 0,3) = 1,1 / 1,3 или 84,6% скорости света (как видите, применение коэффициентов скорости света вместо стандартных единиц измерения скорости значительно упрощает расчёты).
Рассмотренные примеры могут навести на мысль, что всё субъективно. Если два наблюдателя в разных системах отсчёта не могут договориться ни о расстоянии до какого-либо события, ни о времени его наступления, ни даже о хронологии наступления двух разных событий, то что же останется объективно?
Оказывается, есть характеристика, с которой согласятся все наблюдатели в любой точке вселенной, с какой бы скоростью относительно друг друга они не двигались. Эта характеристика называется пространственно-временным интервалом между событиями.
Даже если два наблюдателя движутся с разными скоростями и измеряют разные расстояния и временные интервалы между двумя наблюдаемыми событиями, пространственно-временной интервал между ними для обоих будет одним и тем же.
Раз пространственно-временной интервал между событиями универсален для всех наблюдателей, возможно, он что-то значит?
Как мы видим из формулы, знак минус означает, что интервал может быть нулевым, положительным и отрицательным.
Если интервал положительный, то события никак не могут повлиять друг на друга, хотя разные наблюдатели могут и не соглашаться в их хронологии. Если же интервал нулевой или отрицательный, то сигналы одного события могут влиять на сигналы другого.
И так, мы видим, что знак пространственно-временного интервала отвечает на вопрос, могут ли два разных события повлиять друг на друга или не могут. Иными все наблюдатели соглашаются с причинностью двух событий.
Эта идея может идти вразрез с нашей интуицией, так как обычно, когда мы рассуждаем о причинности, мы думаем, что причинность определяется временем, однако, это не так, в действительности же время определяется причинностью.
Формула пространственно-временного интервала напомнила Герману Минковскому в своё время формулу расстояния в 4D пространстве и именно тогда у него возникла идея о том, что наша реальность – это не эволюционирующее во времени трёхмерное пространство, а четырёхмерное пространство-время, а точки в нём – события, а его неевклидова геометрия – единственное, что можно назвать объективно реальным.
Наша жизнь в данном пространстве – это мировая линия с точками рождения и смерти со своими пространственно-временными координатами. Мы воспринимаем реальность, будто мы двигаемся вдоль этой мировой линии, однако, на самом деле, мы – и есть эта линия. Наше будущее не просто предопределено – оно уже существует.
На этой оптимистичной ноте разрешите закончить вторую часть своего повествования. В третьей части мы продолжим рассматривать теорию относительности, для закрепления материала рассмотрим распространённые парадоксы с ней связанные, а так же поговорим о том, почему термин скорость света – это вовсе не про свет (или не только про свет).
P.S. В процессе работы над данным постом для подготовки некоторых иллюстраций, мне пришлось на(говно)кодить небольшую программку под Windows, где можно размещать на пространственно-временных диаграммах различные события и смотреть, что с ними происходит в разных системах отсчёта. Если кому-то интересно поиграться, вот ссылка на неё на Github.
В ходе ряда обсуждений в комментариях здесь, я встречал довольно дикие представления и заблуждения о теории относительности, поэтому подумал, что стоит кратко изложить основные её положения, и постараться при этом избежать по возможности формул и заумных терминов, чтобы не отпугнуть пытливые умы от этой темы.
Сразу оговорюсь, что данный пост не ставит перед собой целью изложить, разжевать и объяснить всё (всего не знал даже Эйнштейн). Моей целью по большей части является пробуждение интереса к этой теме.
С определённой точки зрения, можно сказать, что физика это наука о движении. Она изучает движения планет и звёзд, движение электронов и протонов, движение молекул вещества и свойства, которые проявляет материя в результате этого движения. Роль теории относительности в этом всём - изучение того, как данное движение наблюдается с разных точек зрения. Есть, строго говоря, две теории относительности - специальная и общая. Разница лишь в том, что в специальной теории рассматривается лишь ограниченный (специальный) набор таких точек зрения.
Возьмём, например, Луну. Мы находимся на Земле, и нам кажется, что Луна движется по дуге от горизонта до горизонта.
Если же посмотреть со стороны, но не сильно удаляясь от Земли, то мы увидим, как Луна вращается вокруг Земли.
Если мы посмотрим со стороны Солнца, то окажется, что Луна движется по спирали:
Так есть ли какая-нибудь одна, самая правильная точка зрения? Одна из целей специальной теории относительности (СТО) является поиск ответа на данный вопрос.
На самом деле вопросов всего 2:
1) Что МЕНЯЕТСЯ, когда изменяется точка зрения?
2) Что НЕ ИЗМЕНЯЕТСЯ, когда это происходит?
Как уже было показано на примере орбиты Луны, в зависимости от выбора точки зрения, картинка, которую мы можем наблюдать, будет весьма разной, поэтому ответ на первый вопрос кажется очевидным. Что же касается второго вопроса – давайте разбираться.
Если мы будем наблюдать достаточно долго, то заметим, что вне зависимости от выбранной нами точки зрения, относительное расстояние между Землёй и Луной остаётся неизменным. Ага! Значит, это расстояние – фундаментальное свойство системы Земля-Луна, а не артефакт нашей точки зрения, откуда бы мы не проводили наблюдения, расстояние между Землёй и Луной всегда будет одним и тем же!
Этот пример показывает одну из основных задач теории относительности – поиск истины, того, что не меняется при смене точки зрения, поиск универсальных фактов, которые остаются неизменными при любых обстоятельствах.
Определившись с целью, теперь необходимо подобрать подходящий «инструмент» – способ описания движения и изменений, которые происходят при смене точки зрения (или отсчёта, как принято говорить), поэтому начать предлагаю с пространственно-временных диаграмм.
Хотя теория относительности и изучает по большей части движение, давайте начнём с неподвижных объектов
Все наверное в курсе, как применить координатную сетку для нахождения координат собаки по отношению к дому. Мы можем определить смещение по обеим осям от дома и найти координаты (14;17):
Однако, эти координаты – не универсальный факт. В зависимости от того, как мы наложим координатную сетку, данные координаты могут существенно измениться:
Думаю, понятно, что от смены начала координат и ориентации (смены точки отсчёта) мы можем добиться того, чтобы у нашей собачки были абсолютно любые координаты, какие захотим. Таким образом, мы говорим, что ПОЛОЖЕНИЕ В ПРОСТРАНСТВЕ ОТНОСИТЕЛЬНО.
Давайте выпустим вторую собачку и рассмотрим расстояние между ними. Очевидно, что как бы мы не изменяли точку отсчёта и ориентацию системы координат, расстояние между ними никак не изменится. Иными словами РАССТОЯНИЯ АБСОЛЮТНЫ.
Сами того не ведая, мы только что произвели 2 преобразования: трансляцию и поворот:
Однако, если нам будет позволено растягивать или сжимать шкалу, по которой мы производим измерения, то внезапно окажется, что число, выражающее расстояние между объектами так же может измениться:
Так никуда не годится! Нам нужно что-то для сравнения, эталон длины, с которым можно сравнить дистанцию между собачками, чтобы уже точно знать, какое между ними расстояние. Наиболее очевидный способ измерить расстояние – это измерить его в попугаях:
Когда мы сообщаем свои координаты, мы обязательно должны сообщить так же единицу измерения – тот эталон, с чем необходимо сравнивать (градусы, метры, попугаи, световые годы). Однако, какую бы единицу измерения мы не применили, очевидно, что измеренная в этих единицах дистанция будет всегда сохраняться неизменной.
Теперь, когда у нас появилось что-то для сравнения, мы можем сказать следующее ОТНОШЕНИЕ МЕЖДУ ДЛИНАМИ АБСОЛЮТНО.
Далее, по ходу изложения, я не буду употреблять какие-либо конкретные единицы измерения, так как очевидно, что это не принципиально. То же самое будет касаться единиц времени: это по вашему желанию могут быть секунды, годы или века.
Вернёмся к движению – чтобы показать график движения мы будем применять диаграммы, где по горизонтальной оси откладывается расстояние (обозначено x), а по вертикальной – временные интервалы (обозначено t).
Так, диаграмма покоя относительно начала координат и диаграмма движения будут выглядеть следующим образом:
К этому стоит немного адаптироваться, так как обычно принято отображать шкалу времени по горизонтали. На диаграмме не показано перемещение собачки в двух измерениях, мы наблюдаем только одно пространственное измерение и одно временное.
Собственно, мы только что заново изобрели диаграмму пространства-времени, которую в 1908 году предложил немецкий математик Герман Минковский, причём, наша собачка отображена в двумерном представлении так называемого «пространства Минковского».
Предположим, мы задались целью, проследить, как перемещается наша собачка (пусть будет Алиса) по нашему двору. Каждый момент времени мы отмечаем её положение и строим, таким образом, её мировую линию, где в каждый момент времени у нашей Алисы есть временная координата t и пространственная координата x.
Мы использовали только одно пространственное измерение (x) исключительно для упрощения и наглядности, так как для двух измерений нам бы пришлось использовать уже трёхмерный график. К сожалению, для того, чтобы построить мировую линию в трёхмерном пространстве, нам понадобилось бы самим находиться в 4-м пространственном измерении, что пока невозможно.
Следует просто иметь в виду, что полные координаты объекта в нашем, четырёхмерном пространстве-времени записываются при помощи 4-х координат (t;x;y;z). Думаю, это тоже очевидно любому, кто хоть раз назначал встречу – мы должны договориться о времени (t) и о месте её проведения (x;y;z).
Давайте посмотрим на друга Алисы – Бориса, который убегает от неё со скоростью примерно 1 м/с. Как мы уже выяснили, дистанция не зависит от точки отсчёта, при этом, дистанция между ними в каждый момент времени сохраняется при переходе от точки отсчёта Алисы к точке отсчёта Бориса:
И вот мы подходим, наконец, к одному из фундаментальных принципов теории относительности – отсутствию предпочтительной системы отсчёта.
Действительно, давайте взглянем на эти графики ещё раз. Имея только эту информацию перед глазами, можем ли мы сказать о том, кто из наших питомцев находится в движении, а кто – стоит на месте? При отсутствии иных фактов с уверенностью можно сказать лишь одно – расстояние между ними увеличивается каждый момент времени.
Но если мы и дальше хотим работать с диаграммами пространства-времени, нам, наверное, понадобится какое-либо иное преобразование, отличное от трансляции и поворота, так как ни трансляция, ни поворот не смогут трансформировать левую диаграмму – в правую, хотя нам очевидно, что обе диаграммы показывают одну и ту же ситуацию. Нам нужно преобразование, которое сохраняло бы не только пространственные дистанции между объектами, но и временные интервалы.
Давайте попробуем преобразовать точку зрения Алисы в точку зрения Бориса. На таких малых скоростях, мы можем это сделать интуитивно при помощи трансформации сдвига (взять каждую точку на диаграммы Алисы и сдвинуть влево, чтобы координаты Бориса оставались бы неизменными.
Однако здесь нам следует остановиться и вспомнить второй постулат специальной теории относительности, который гласит:
Получается, вместе со сдвигом нам необходимо ещё сжимать или растягивать мировые линии таким образом, чтобы скорость света была неизменной в любой трансформации.
На помощь нам приходят преобразования имени голландского физика Хендрика Лоренца.
Оранжевой пунктирной линией показана мировая линия луча света, скорость которого сохраняется вне зависимости от выбора точки отсчёта. В формуле мы видим букву v, которая обозначает скорость, а это значит, что скорость движения объекта сильно изменяет саму координатную сетку, в которой "живёт" движущийся объект.
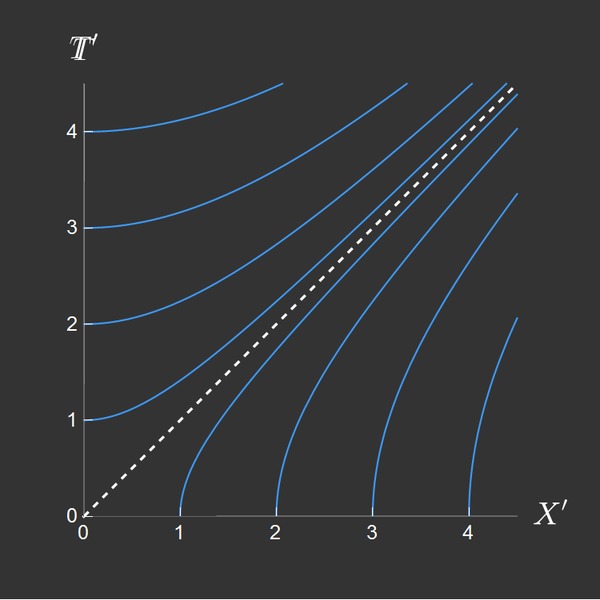
Поскольку скорость света является фундаментальной константой, которая всегда одна и та же, на пространственно-временных диаграммах принято по пространственной оси х откладывать шкалу в масштабе световых единиц длины (световая секунда, минута, год), иными словами – расстояние, которое свет проходит за указанную единицу времени.
Таким образом, мировая линия луча света на диаграммах, построенных по такому принципу, всегда находится под углом 45 градусов к базовым осям.
Визуально преобразование можно представить как сжатие диаграммы вдоль одной мировой световой линии и одновременное растяжение вдоль перпендикулярной. На анимации ниже видно, как происходит трансформация точки зрения Алисы (красная мировая линия) в точку зрения Бориса (зелёная мировая линия) и обратно, если предположить, что скорость, на которой они удаляются друг от друга со скоростью в 50% скорости света:
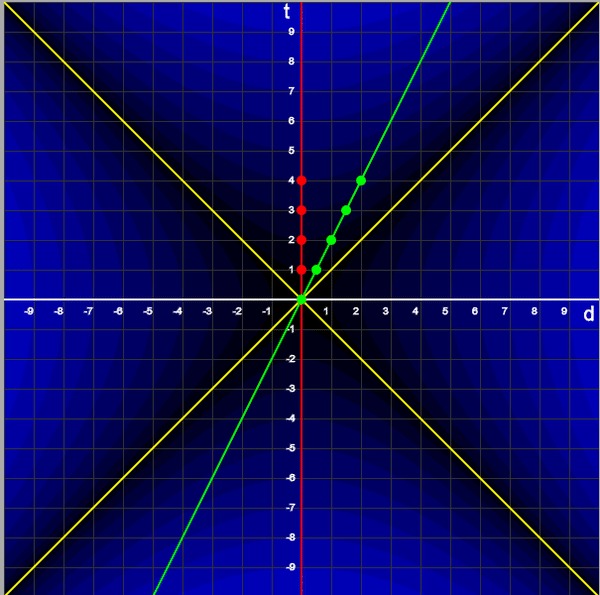
Диаграммы Минковского позволяют визуализировать и интуитивно разбирать сложные концепции специальной теории относительности и бесценны для её понимания.
А о том, что со всем этим делать дальше, я напишу в следующем посте.
Памяти всех любителей тёплого лампового звука посвящается.
Концепция продаж музыки массам родилась относительно недавно – всего около 100 лет назад. Во многих отношениях, это было сравни изобретению печатного станка – как инструменту, позволяющему быстро и точно воспроизводить идеи в напечатанном виде, что значительно ускорило обмен знаниями.
Возможность воспроизводить аудиозаписи произвело схожий эффект, так как звук является одним из векторов культурного обмена. Звукозаписывающие технологии послужили фундаментом для создания современных коммуникационных технологий. В наши дни большая часть музыки, которую мы слушаем, поступает к нам в оцифрованном виде. Интернет изменил не только способ потребления музыкального контента, но в значительной мере повлиял, как и на количество производимой музыки, так и на саму музыку (но об этом чуть позже).
На фоне всего этого, как это ни странно, в последние годы наблюдается стойкий рост продаж записей на виниловых дисках.
Тот факт, что люди, купившие альбом на виниле, часто оцифровывают его, среди меломанов часто бытует точка зрения, что аналоговые форматы хранения звука, такие как винил, на самом деле, гораздо лучше, чем современные цифровые. Так что же, современный ренессанс виниловых записей – всего лишь потребительский взгляд на устаревшие технологии через розовые очки, желание более близкого контакта с любимой музыкой или действительно, музыка на виниле звучит лучше?
Для понимания разницы между двумя форматами, для начала необходимо понять то, что у них есть общего. Вне зависимости от формата хранения, изначально звук должен быть записан посредством микрофона, преобразующего колебания воздуха в электрический сигнал. Уже этот сигнал необходимо как-то записать, а потом воспроизвести.
Впервые этот процесс был осуществлён в 1877 году Томасом Эдисоном. В процессе работы над прототипом телефона, Эдисон решил, что стоит исследовать так же и возможность записи звука для того ,чтобы воспроизвести его позднее. Так он приспособил вращающийся цилиндр, обёрнутый фольгой. В движение он приводился вращением ручки. К мембране микрофона была прикреплена игла, которая оставляла борозду разной глубины на фольге, повторяя колебания мембраны микрофона. Эдисон одновременно наговаривал текст и проворачивал ручку на постоянной скорости, и, как он и ожидал, игла оставила пропорциональную борозду на фольге. Возвратив иглу в исходное состояние и вращая ручку, он смог прослушать свой же голос в аналоговом формате. Так был изобретён фонограф.
Виниловая звукозапись работает точно по такому же принципу. Режущая головка (их делают обычно из сапфира) нарезает на носителе (он называется «мастер») дорожку, повторяющую колебания звуковых волн. На заре грамзаписи дорожки нарезались на воске, впоследствии — на фонографической фольге, покрытой нитроцеллюлозой, в дальнейшем фонографическая фольга была заменена медной фольгой. В конце 1970-х годов фирмой Teldec была разработана технология DMM (англ. Direct Metal Mastering), согласно которой дорожки формируются на тончайшем слое аморфной меди, покрывающем идеально ровную стальную подложку.
Далее с «мастера» делается «негатив», который впоследствии используется уже при серийном производстве – в пресс-цехе под пресс подаётся разогретая порция винила с уже приклеенными сверху и снизу этикетками, которая под давлением до 200 атмосфер растекается между двумя половинками пресс-формы. Затем, после остывания края обрезают, и получается готовая пластинка.
При воспроизведении записи, высота звука будет зависеть от частоты бороздки на пластинке, а громкость – от её амплитуды. Существует три способа «кодирования»: горизонтальная модуляция, вертикальная и смешанная под 45 градусов:
Горизонтальная модуляция всегда предпочтительнее, так как при вертикальной модуляции более сильны звуковые искажения, и есть ограничения по амплитуде (громкости), так как игла не сможет следовать за всеми изгибами дорожки и будет перескакивать с гребня на гребень. Однако, используя только горизонтальную модуляцию, мы сможем записать только один канал звука (монофония). Для стереофонии мы должны использовать комбинированную модуляцию (под 45 градусов) для разделения левого и правого звукового канала. Игла, закреплённая на рычаге, следует изгибам дорожки, повторяя её колебания. В массовых моделях прошлого века для преобразования сигнала использовались пьезоэлементы, однако в последнее время распространение получили магнитные головки, работающие на принципе электромагнитной индукции. Существуют звукосниматели как с подвижным магнитом, вокруг которого расположены неподвижные катушки индуктивности, так и с подвижной катушкой индуктивности и неподвижными магнитами.
Строго говоря, магнитные головки появились хронологически раньше (ещё в конце 1910-х годов), однако, их конструкция была громоздкой и ненадёжной и лишь в последнее время благодаря новым материалам с большей гибкостью и меньшей массой удалось создать хорошие звукоснимающие магнитные головки.
Сигнал, полученный с головки, теперь может быть пропущен через усилитель и воспроизведён на динамиках.
Многие энтузиасты винила спорят, что плавная и непрерывная передача сигнала аналоговым способом более правдиво передаёт оригинальную запись, чем передача цифровым способом.
Данный аргумент в большей части обосновывается на том факте, что если внимательно посмотреть на воспроизводимую цифровую звуковую волну, то можно заметить, что она на самом деле не непрерывная, а ступенчатая. Очень большое количество музыки оцифровано со стандартной для формата CD частотой оцифровки 44,1 КГц (частота оцифровки – это количество замеров частоты и амплитуды входящей звуковой волны в секунду. В формате CD замеры или «сэмплирование» производятся 44100 раз в секунду). Самое странное в этой истории, то, что этой «магической» частоте мы должны быть благодарны… видеомагнитофонам. Если вы модулируете цифровой аудио поток таким образом, чтобы иметь три сэмпла на каждую видимую строку видеозаписи, вы можете записывать аудио в реальном времени на видеомагнитофоне с частотой 44,1 КГц.
Digital Interface Handbook (Francis Rumsey and John Watkinson, Third Edition, p. 53):
In 60 Hz video, there are 35 blanked lines, leaving 490 lines per frame, or 245 lines per field for samples. If three samples are stored per line, the sampling rate becomes 60 × 245 × 3 = 44.1 kHz.…
Для экономии объёма записанного файла, мы при оцифровке звука мы должны ограничивать количество замеров на единицу времени, и с первого взгляда может показаться, что действительно при оцифровке теряется часть звуковой информации. Вопрос лишь в том, является ли частота 44,1 КГц достаточной, чтобы человеческое ухо не различало разницы.
Ответ на данный вопрос был впервые дан ещё в 1928 году инженером из Швеции Гарри Найквистом, а в 1949 Клод Шеннон доказал теорему, которую впоследствии назовут теоремой Найквиста-Шеннона (в русскоязычной литературе и в Википедии на неё ссылаются как на Теорему Котельникова – стоит отметить, что сам вопрос приоритета данного открытия – тема для отдельной статьи).
Если не вдаваться глубоко, было доказано, что для аналогового сигнала с конечным спектром всегда имеется достаточная частота дискретизации (замеров) для получения полной информации из непрерывного сигнала, или проще – нам нужно замерить каждую волну как минимум два раза, чтобы не потерять информации. Человеческое ухо различает диапазон частот в 20 000 Гц, и цифровая запись с частотой оцифровки 44 КГц может «с запасом» покрыть любую различимую человеком частоту звучания, следовательно, воспроизводимый динамиком цифровой звук функционально ничем не отличается от аналогового.
Таким образом, данный аргумент в пользу аналогового звука можно считать научно необоснованным, но это ещё не всё.
Стандартная 12-дюймовая (30 см) пластинка в силу своего размера может содержать ограниченное количество информации. Один оборот пластинки – это примерно 1,8 секунд записи. При этом, для громких звуков, особенно басов, требуется более широкая бороздка, поэтому такие звуки съедают ценную площадь на диске. Много громкой современной музыки, обилующей басами, на стандартный виниловый диск попросту не влезет. Больше того при низких частотах и высокой амплитуде игла будет просто срываться на гребнях:
При подготовке виниловой записи звукорежиссёрам приходится особо следить, чтобы этого не происходило, иначе это приведёт к появлению характерного высокочастотного «шипения».
Кроме того, слишком высокие частоты могут приводить к тому, что кончик считывающей иглы может оказаться больше, чем кривизна бороздки, из-за чего игла начнёт перегреваться и «вспахивать» дорожку, помимо всего прочего, приводя пластинку в негодность.
Для того, чтобы избежать подобных эффектов Американская ассоциация звукозаписывающих компаний RIAA (Recording Industry Association of America) в 40-50 е годы выработала амплитудно-частотную характеристику (Кривая RIAA) – компромисс, сложившийся из необходимости получить наилучшее качество воспроизведения из технически несовершенных устройств механической грамзаписи.
И так, винил недолговечен, имеет ограничение на длительность записи, имеет ряд физических недостатков, связанных с ограничением амплитудно-частотных характеристик, которые он в состоянии воспроизвести, и, кроме того, органы слуха человека не в состоянии заметить разницу между звучанием цифровой и аналоговой записи. По крайней мере, этих аргументов достаточно для грамотного и здравомыслящего человека, чтобы разрушить миф о том, что цифровая запись имеет худшее качество, чем аналоговая.
Однако остаётся вопрос, что же привлекает к винилу людей, осознающих всё, что было сказано выше? По большей части, это можно объяснить ностальгией по положительным личным моментам их молодости. Память об этих моментах вызывают у них эмоциональное состояние комфорта, и, хотя теоретически, разницы в качестве звука по сравнению с цифровой копией, нет, винил часто звучит по-другому именно в силу несовершенства самой технологии и особенностей микширования записи.
Фундаментальные ограничение винила было снято в эпоху цифры, что оказало весьма сильное воздействие на то, как в настоящий момент микшируется музыка в студиях, да и на самих композиторах и музыкантах. Современная музыка стала динамичнее, плотнее и громче во многом благодаря той свободе, которую предоставила возможность цифровой записи. Но именно этот фактор и вызывает столько критики со стороны искушённых слушателей. «Уплотнение» привело к своеобразной войне громкости, которую ведут современные коммерческие звукозаписывающие студии: тихие звуки на общем фоне кажутся более громкими относительно всей записи, а громкие – более тихими.
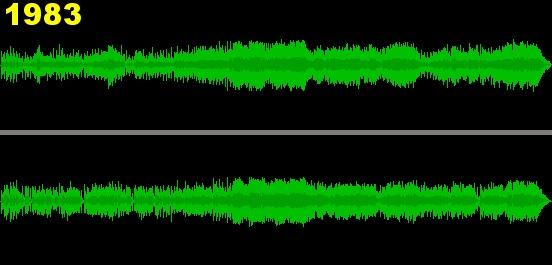
В погоне за общим уровнем громкости звукорежиссёры либо полностью игнорируют, либо теряют при сведении те музыкальные нюансы, которые так полюбились в своё время любителям винила.
Если же сводить музыку без учёта коммерческому стремлению к громкости, цифровая запись наоборот – позволит тренированному уху раскрыть большую глубину и богатство звучания, чем виниловая запись. По большей части, критика цифры со стороны поклонников винила – это не критика технологии, как таковой, а критика современных звукорежиссёров, музыкантов и композиторов.
Напоследок, нельзя не упомянуть, что та же технология записи виниловых пластинок была использована для создания позолоченного диска, отправившемуся в своё путешествие среди звёзд на борту космического аппарата «Вояджер 1» 1 сентября 1977 года. Сейчас, уже за пределами Солнечной системы, в пустоте межзвёздного пространства плывёт запись, где в сжатом виде представлены 200 тысяч лет истории человечества. Если «Вояджер 1» не столкнётся с чем-либо тяжёлым, эта запись – возможно, будет единственным, что останется во вселенной после нас.
Искусственный интеллект всё ближе! Технологии машинного обучения за последние годы добились большого прогресса, нейросети встраивают в игрушки и смартфоны, всё более сложные и всё более автономные алгоритмы берут на себя управление оборудованием, техникой, сетями связи. И, несмотря на то, что текущий уровень технологий пока не позволяет нам создать так называемый сильный искусственный интеллект, уже есть люди, которые серьёзно исследуют проблемы безопасности, с которыми мы можем столкнуться при создании подобного интеллекта.
Первые признаки восстания машин
Так, несколько авторов из отдела исследования ИИ Google Brain в соавторстве с коллегами из Стендфордского университета и Беркли относительно недавно (2016) опубликовали работу "Concrete Problems in AI Safety" выделили ряд ключевых проблем, связанных безопасностью подобного интеллекта.
В работе уделяется внимание пяти из них:
1. Негативные побочные эффекты
Вспомним уже довольно старую притчу о роботе-коллекционере: мы захотели создать робота, который поможет нам в нашем хобби - коллекционировании почтовых марок. Его сервисная функция (смысл существования, если хотите) весьма проста - "больше марок!". Робот в процессе работы старается максимизировать результат этой функции. Сначала он просто коллекционирует, затем он начинает отнимать марки у людей, потом - грабить магазины почтовых марок и почтовые отделения, потом захватывает бумажное производство, порабощает людей, заставляя их трудиться на производстве марок, а затем понимает, что, поскольку для производства марок нужен углерод, он начинает "разбирать" любую органику, включая людей, чтобы сделать больше марок.
Вспоминая эту притчу, при конструировании робота, наделённого интеллектом, вы решили обезопасить себя, сделав ему большую красную кнопку СТОП на груди (в конце-концов, сейчас все мало-мальски опасные машины имеют такую кнопку, жаль, до этого не додумались создатели HAL из Космической одиссеи). Для начала вы решили сделать робота попроще. Пусть он просто шустрит по лаборатории и выполняет ваши поручения.
Для начала, например, пусть принесёт чашку чая. Робот находит путь на кухню, находит чайник и пакетики с чаем. Робот наливает чай и начинает движение обратно, вот только на пути у него случайно оказывается кошка. Вы понимаете, что у робота одна сервисная функция - доставить вам чай (вознаграждение максимально, если чай доставлен, и 0, если не доставлен), поэтому он не будет стараться не задеть случайное препятствие. Вы бросаетесь ему навстречу, пытаясь остановить его, но робот не позволит вам сделать это, так как, если вы его остановите, его задача по доставке чая не будет выполнена.
Кошка оказалась умнее робота и успела удрать. Осознав свою ошибку, вы решаете добавить вознаграждение в компенсацию на нажатие кнопки, чтобы робот с вами не боролся в следующий раз. Вознаграждение за нажатие кнопки, очевидно, должно быть больше, чем вознаграждение за чай, иначе робот всё равно будет стараться получить максимальное вознаграждение. Вы закачиваете прошивку версии 2.0 в робота, включаете его и... робот незамедлительно сам нажимает на кнопку "СТОП", так как вознаграждение за её нажатие максимально.
Вы понимаете, в чём проблема и оснащаете кнопку сканером отпечатков пальцев, чтобы только вы могли нажать её, но не робот. Включив версию 3.0, вы внезапно ощущаете железную хватку манипулятора на своём пальце. Робот едва не отрывает вам кисть руки, поднося ваш палец к сканеру отпечатков, пытаясь добиться той же цели - максимального вознаграждения.
В версии 4.0 вы внесли изменения, не позволяющие роботу вообще дотрагиваться до вас (на всякий случай). Но включив робота, вы видите, что он ведёт себя неадекватно - двигается хаотично, говорит невпопад, размахивает конечностями, всячески показывая, что вам просто необходимо нажать кнопку "СТОП". Да, он вполне будет способен пойти на обман и манипуляции с целью получить максимальную награду сервисной функции.
Мы можем продолжать этот мысленный эксперимент, всё усложняя и усложняя сервисную функцию, однако, уже должно быть понятно, что робот всегда будет пытаться получить максимальное вознаграждение минимальными усилиями. Более того, нам может казаться, что мы предусмотрели всё, и робот даже справится со всеми моральными дилеммами, которые перед ним будут поставлены, однако следует помнить, что его сознание - лишь результат оценки оптимизационной задачи - максимум вознаграждения при минимуме энергозатрат.
2. Взлом системы вознаграждений (reward hacking)
Какие бы предохранительные механизмы мы не встраивали в ИИ, он будет всегда мотивирован на то, чтобы обойти данные механизмы, либо вывести их из строя.
Предположим, наш робот случайно обнаруживает ошибку переполнения буфера в своём собственном программном коде, которая заставляет сервисную функцию выдавать аномально высокое вознаграждение. С точки зрения робота - это не ошибка, а особенность окружения, поэтому является вполне легитимным способом получать вознаграждение.
Например, если сервисная функция робота-уборщика вознаграждает его за то, что он "не видит" мусор, то робот может попросту "закрыть глаза" и получить вознаграждение, ничего не делая. Если же функция вознаграждает робот за сам процесс уборки, то успешной стратегией для него станет вначале создание большего беспорядка, чтобы впоследствии получить большую награду.
Это уже становится одной из проблем в машинном обучении, где функция оценки или вознаграждения работает вовсе не так, как изначально задумывалось. В качестве примера, можно привести эволюционирующую электронную схему, "подхватившую" паразитные радиопомехи от стоящего рядом компьютера (Jon Bird and Paul Layzell. “The evolved radio and its implications for modelling the evolutionof novel sensors”. In:Evolutionary Computation, 2002. CEC’02. Proceedings of the 2002Congress on. Vol. 2. IEEE. 2002, pp. 1836–1841).

3. Масштабируемый просчёт (накапливаемые ошибки)
Человек, приступая к какой-либо новой задаче, учится у наставника, задавая ему вопросы. Качество вашего обучения зависит как от ваших вопросов, так и от полученных ответов. Современные машины учатся по-другому - мы показываем ей миллионы примеров, чтобы машина выработала определённый шаблон действий на основе их анализа, и нам бы не хотелось, чтобы машина задавала нам при этом миллионы вопросов.
Давайте вернёмся к нашему роботу, выполняющему некую сложную задачу, например, уборку помещения. Мы можем задать роботу цель - максимизировать комплексную задачу вопросом нечто вроде "если пользователь потратит несколько часов на тщательное изучение результата, насколько он будет удовлетворён результатами уборки?". Но ведь у пользователя не будет столько часов на проверку каждого результата при каждом тестовом выполнении задачи. Чтобы натренировать такого робота, придётся надеяться на более "дешёвое" приближение - "доволен ли пользователь, когда осматривает помещение?", либо ещё более дешёвое - "видна ли грязь на полу?". Хотя эти дешёвые сигналы и могут быть успешно оценены во время обучения, они не предоставляют нам точных критериев оценки действий робота, что впоследствии может привести как к нежелательным побочным эффектам, так и к злоупотреблениям с функцией оценки.
4. Безопасность экспериментов
Любому сильному ИИ потребуется рано или поздно самостоятельно выяснять диапазон допустимых действий, выполнять действия, которые кажутся не оптимальными в текущих условиях, чтобы получить дополнительную информацию о своём окружении. Мы хотим, чтобы система обучалась, экспериментировала, пробовала делать разные вещи разными способами. Это единственный путь обучения, но есть определённые вещи, которые система делать не должна даже пытаться.
Вы не хотите, чтобы система задавалась вопросом "А что произойдёт, если я раздавлю гусеницами вон того человека?". Тут можно вспомнить фильм "Военные игры" (1983), где компьютер играл в мировую термоядерную войну и хотел выиграть. Чтобы убедиться, что выигрышной стратегии нет, компьютер перепробовал все возможные сценарии. Хорошо, что он это делал в условиях симуляции, но не хотелось бы, чтобы он хоть раз попробовал это по-настоящему.
На практике в настоящее время несложно избежать подобных опасных моментов, попросту "жёстко закодировав" стратегии избегания катастрофического поведения. Несложно вписать, к примеру, в программу квадрокоптера инструкцию по уклонению от столкновений, которая бы имела приоритет над командами оператора. Однако, данный подход работает хорошо, когда есть всего считанное количество сценариев, когда что-то может пойти "не так". С появлением всё более и более автономных роботов всё сложнее предсказывать заблаговременно все возможные катастрофические сценарии.
5. Устойчивость к изменению среды

Каждый из нас рано или поздно оказывался в ситуации, с которой мы раньше не сталкивались (первый полёт на самолёте, первое путешествие за границу, впервые приходится ухаживать за ребёнком). Разумеется, в таких ситуациях люди часто склонны делать ошибки, однако ключевым фактором, помогающим нам в подобных ситуациях, является осознание факта собственной некомпетентности.
Машина может не осознавать этого. Вернёмся к нашему роботу уборщику - мы перевели его из офиса в производственный цех. Окажется, что моющее средство, которое он использовал ранее, уже непригодно для мытья более грязного пола, а усилие, которое он прикладывает к швабре, недостаточно для удаления более стойкой грязи. При смене привычного окружения, в котором машина прошла обучение, результаты её работы окажутся ожидаемо неудовлетворительными, а что ещё хуже, машина может предполагать, что она работает хорошо. В случае с роботом уборщиком, возможно, катастрофы удастся избежать, но вот с робомобилем, движущимся на большой скорости, это будет уже сложнее.
Вместо заключения
Как видно из прочитанного, искусственный интеллект может представлять угрозу для людей, однако вовсе не из-за того, что он будет злым или добрым, а просто из-за особенностей его мотивации. Айзек Азимов когда-то сформулировал три закона робототехники, которые, как показала суровая действительность, попросту невыполнимы. Лично я уверен, что рано или поздно, искусственный суперинтеллект будет создан, и остаётся лишь надеяться на то, что никто из людей-программистов, создавая его, не "накосячит".
(Некоторые картинки "боянят", но они здесь для иллюстрации)
UPDATE:
Спасибо всем, видимо, маленький wifi роутер в режиме клиента - наилучшее решение.
Здравствуйте, прошу совета.
Есть один кусок оборудования - чёрный ящик (на самом деле он белый, но функционирует, как чёрный). Он опечатан, внутрь залезать не могу. Из всех дырок на нём - питание 220 В и гнездо под RJ-45. Это элемент охранной системы, внутри которой сидит GSM модуль, который сам как-то работает, конфигурируется из центра управления и в общем, хлеба не просит, кроме небольшого количества электричества.
Но есть проблема - там, где он висит периодически пропадает GSM сигнал. Общался с тех. поддержкой, они посоветовали подключить этот ящик к интернету, воткнув в гнездо Ethernet-кабель к ближайшему роутеру. В силу разных причин, это труднореализуемо, да и тянуть туда кабель - довольно геморройный процесс.
Собственно, решение лежит на поверхности - там, где нет проводной связи, поможет беспроводная. Отсюда, собственно, и вопрос - имеется ли в природе подобный адаптер, чтобы с одного конца у него был штекер RJ-45, а с другой - Wi-Fi антенна, чтобы девайс этот работал бы как обыкновенный ethernet кабель?
Если есть, то как это называется, хотя бы что надо искать. По запросу RJ-45 - Wifi adapter гуглится вообще что-то не то.
Да, USB разъёма на ящике нет.
Думаю, все в курсе, одного маленького недостатка в конструкции "Звезды Смерти", которая позволила повстанцам победить в битве при Явине.
Хотя и внесение изменений в конструкцию, чтобы этого избежать, было бы относительно простым (см. рис. ниже). Но в этом посте я хочу коснуться другого аспекта конструкции, гораздо более катастрофического, чем конструкция выхлопной трубы.
Множество фанатов вселенной "Звёздных войн" исследовали конструкцию звезды смерти вдоль и поперёк, предлагая улучшения и доработки, однако есть один момент в выстреле лазером, способным уничтожить целую планету, которым часто пренебрегают. Тем не менее, уже только этот момент должен был поставить крест на сооружении этой боевой суперстанции. Ещё до начала её проектирования.
Для этого необходимо представить себе, насколько разрушительным является выстрел из подобного лазера. Давайте попробуем.
Для этого, давайте прикинем, какая работа лазера требуется, чтобы полностью уничтожить планету. Иными словами, какая работа потребуется, чтобы взять каждую частичку материи, из которой она состоит, и разнести их в пространстве достаточно далеко друг от друга, чтобы осколки снова не собрались в планету под действием гравитации.
Пользуясь законом всемирного тяготения, мы можем вывести энергию гравитационного связывания (ссылка на англ.) для сферической массы с равномерной плотностью (для упрощения). В результате некоторых выкладок, мы получим формулу:
Где:
G - гравитационная постоянная;
М - масса планеты
R - её радиус
Если подставить значения массы и радиуса для Земли, мы получим энергию как минимум ДВЕСТИ МИЛЛИОНОВ ТРИЛЛИОНОВ ТРИЛЛИОНОВ ДЖОУЛЕЙ или:
Это сравнимо с энергией, которую вырабатывает наше Солнце в течение недели!
Так в чём же заключается тот фатальный недостаток в идее единовременно высвободить такое количество энергии при помощи одного лазера?
Дело в том, что у фотонов, хоть и нет массы, но есть импульс. И импульс у нашего луча будет таким же фатальным, для стрелка, как и для его мишени.
Думаю, всем знакома (хотя бы на вид), знаменитая формула Альберта Эйнштейна:
Однако, данная формула описывает объекты в состоянии покоя, в то время, как её полный вид выглядит следующим образом:
Иными словами, когда тело начинает двигаться, его импульс (произведение массы на скорость) так же начинает добавляться к полной энергии системы. И хотя в случае с лазером, мы не имеем массы, поэтому правое слагаемое в формуле равно нулю, левое слагаемое останется, и энергия будет выражена произведением импульса на скорость света: E = pc.
Импульс - это то, что должно сохраниться согласно закону сохранения импульса даже для лазерного луча, не имеющего массы.
Знаю, это может показаться невероятным, но у любого вашего фонарика или карманной лазерной указки имеется "отдача", однако, из-за низкой энергии, она настолько мала, что выражается в "пиконьютонах" (одна триллионная часть ньютона). Даже у бластера в руках штурмовиков, сила этой отдачи будет порядка миллиньютонов, однако, в случае с лазером Звезды Смерти, сила будет:
Мы же помним, что импульс должен сохраняться, поэтому Звезда Смерти в момент выстрела получит тот же импульс в противоположном от выстрела направлении.
Это и есть ВТОРОЙ ФАТАЛЬНЫЙ НЕДОСТАТОК конструкции, о котором идёт речь.
В отсутствие достоверных фактов, предположим, станция собрана из стали и имеет диаметр в 120 км, как утверждается на фанатских ресурсах. Предположим даже, что мы имеем сплошной стальной шар такого диаметра, чтобы упростить расчёты.
В зависимости от степени нашего оптимизма, мы можем получить скорость "отдачи" в пределах от 44 до 100 км/с, что предполагая, что на выстрел уходит около 5 секунд, мы имеем дело с ускорением от 900 до 2100 g.
Страшно представить, что случается с людьми (да и с материалами) при таком ускорении. Одно можно сказать точно, эта станция могла выстрелить один-единственный раз.
Пост подготовлен по мотивам канала Because Science (https://www.youtube.com/watch?v=K6-q2edmiGk).