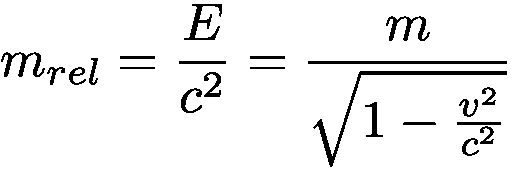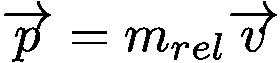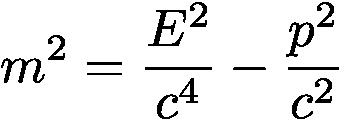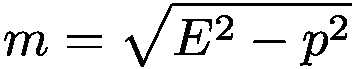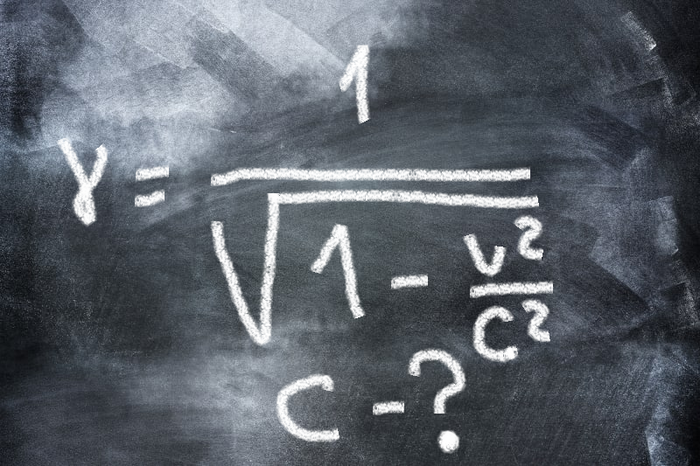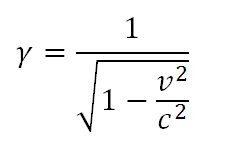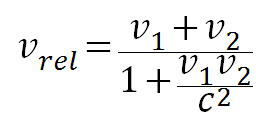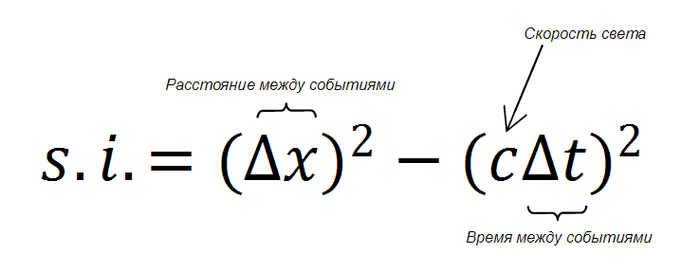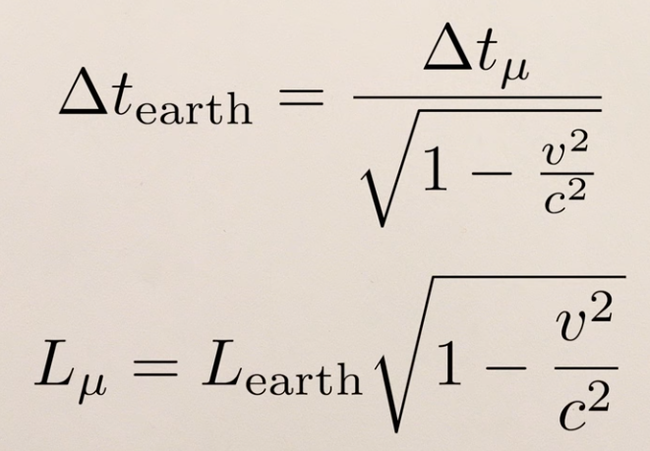Серия «Теория относительности»

Продолжение.
Часть 1
Часть 2
Часть 3

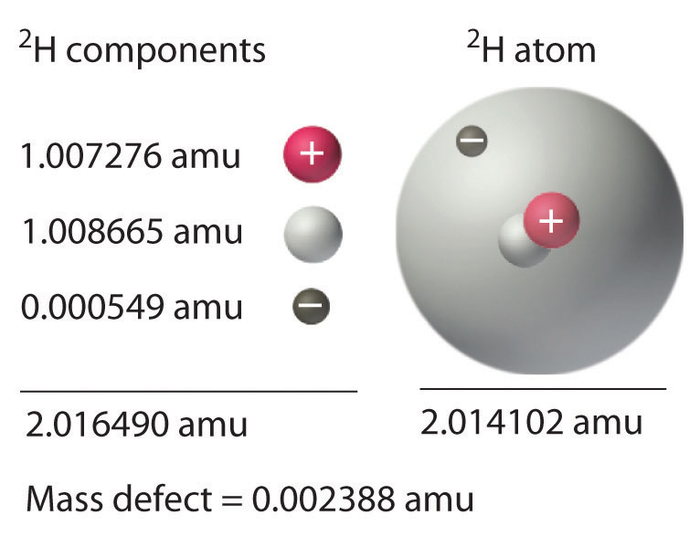
Атом водорода имеет меньшую массу, чем сумма масс отдельно взятых протона и электрона. Мы знаем это точно, иначе бы в нашей Вселенной не было бы звёзд, потому что именно благодаря этому «дефекту массы» и возможны ядерные и термоядерные реакции, однако, как может что-то иметь массу меньшую, чем сумма масс его составных частей?

Разумеется, из за этого:

Давайте посмотрим, что же на самом деле означает самое знаменитое уравнение в истории физики.

Это уравнение было опубликовано А. Эйнштейном 27 апреля 1905 года в работе под названием «Зависит ли инерция тела от содержащейся в нем энергии?», где заключается: « … если тело отдаёт энергию L в виде излучения, его масса уменьшается на L/c² ». Иными словами, в оригинале, уравнение имело вид:

m = L/c²

(в оригинальной работе Эйнштейи использовал для энергии обозначение L)
Русский перевод здесь, всего 3 странички, можно осилить.

Эйнштейн использовал такую запись, потому что краеугольным камнем современной физики является понимание того, что такое масса.

Мы часто слышим утверждения вроде масса – одна из форм энергии, или масса – «замороженная» энергия, или (в наихудшем виде) масса может быть преобразована в энергию. На самом деле ни одно из данных утверждений не верно на 100%.

Чтобы понять, что же именно значит E = mc², давайте рассмотрим явления, которые не укладываются в наше повседневное и обыденное представление о массе.

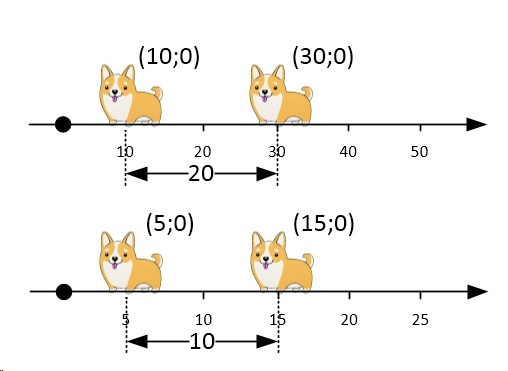
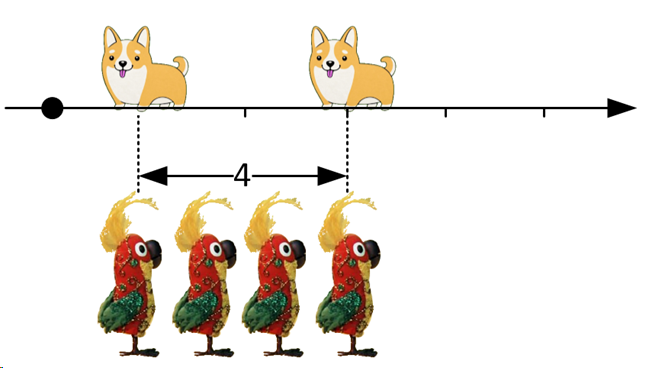
Вот, к примеру, одно из них: если два объекта состоят из абсолютно идентичных составных частей, данные объекты не обладают идентичной массой.

(a + b + c) ≠ (b + c + a)

Масса чего-либо созданного из более мелких составных частей не является суммой масс этих частей:

m1 ≠ ma + mb + mc
m2 ≠ ma + mb + mc

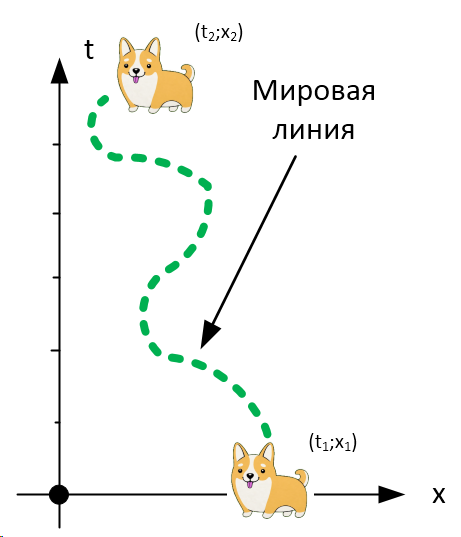
Общая масса составного объекта зависит во-первых, от того, как составные части расположены по отношению друг к другу, во-вторых – от того, как они двигаются внутри данного объекта.

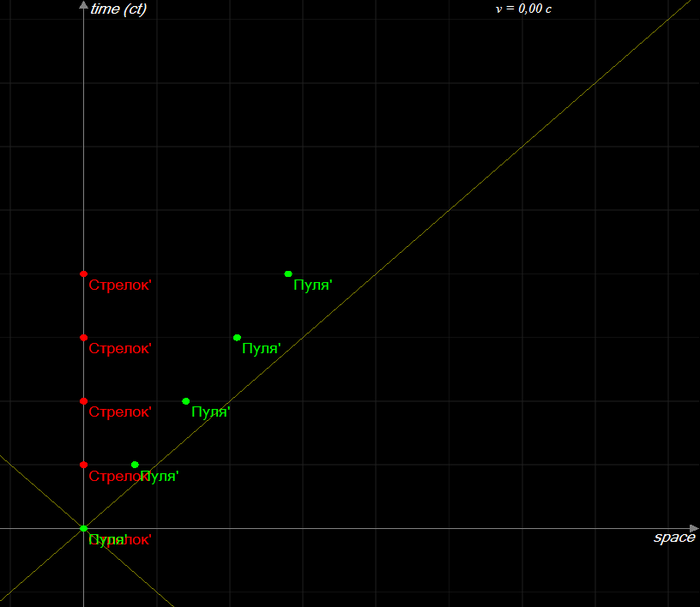
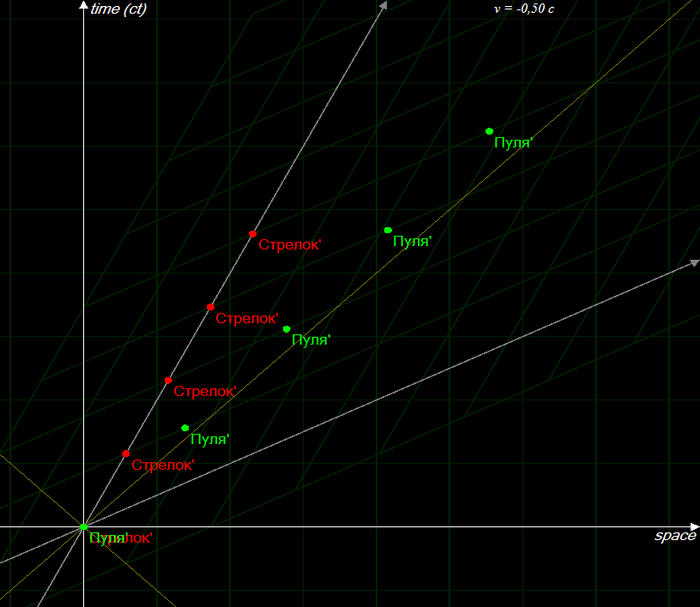
Вот конкретный пример: представьте себе пару заводных механических часов, чьё строение идентично до атомной структуры. Единственная разница между ними – то, что пружина в одних часах взведена, и часы идут, а пружина вторых часов расслаблена, и часы стоят. Согласно Эйнштейну, масса тикающих часов больше, потому что шестерёнки и стрелки находятся в движении и их кинетическая энергия больше. Кроме того, пружина в этих часах заведена и имеет большую потенциальную энергию. Между движущимися деталями этих часов возникает трение, которое их слегка нагревает, и атомы, из которых состоят эти часы, двигаются более интенсивно. Тепловая энергия – это та же кинетическая энергия атомов, из которых состоят наши часы.

Так что же говорит нам уравнение E = mc²? То, что вся тепловая, кинетическая и потенциальная энергия часов добавляется к их массе. Мы просто складываем всю эту энергию, делим на скорость света в квадрате и получаем ту «лишнюю» массу, которая добавилась к идущим часам.

Так как величина скорости света в квадрате – астрономически огромное число, полученное нами значение даст прибавку порядка атто-грамм или 1×10⁻¹⁸ доли процента (0,000000000000000001%), однако эта разница в массах присутствует и может быть объективно-измерена в лабораториях.

Этот пример показывает нам, что масса – это не характеристика количества материи в объекте. В повседневной жизни мы просто не замечаем разницы.

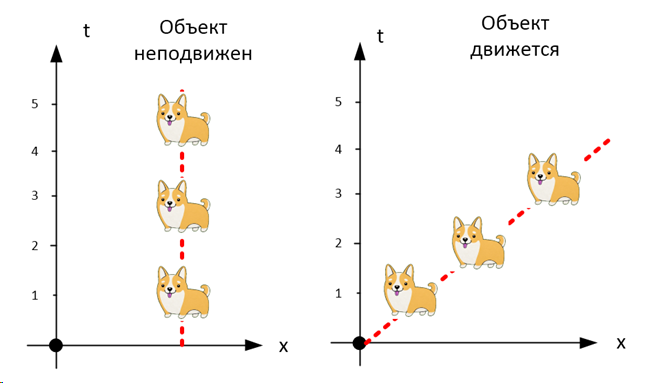
Для того, чтобы среди физиков не возникало недопониманий, современная наука оперирует понятием «масса покоя» или «инвариантная масса», то есть – масса недвижимого объекта. Само слово «покоя» часто не произносят, но когда говорят о массе, всегда подразумевают «массу покоя», так как только о данной величине все независимые наблюдатели из любой системы отсчёта смогут договориться (по аналогии с тем, как пространственно-временные интервалы между событиями являются единственной объективной характеристикой, о которой могут договориться независимые наблюдатели).

Из классической ньютоновской механики мы знаем, что полная энергия движущегося объекта растёт, что выражается формулой кинетической энергии E = mv²/2, путём нехитрых преобразований мы можем получить понятие релятивистской массы – массы движущегося тела:

Таким образом, релятивистская масса является коэффициентом пропорциональности между импульсом и скоростью тела:

Поскольку импульс тела так же вносит свой вклад в полную энергию (и релятивистскую массу), полная версия уравнения Эйнштейна выглядит следующим образом:

Определённая таким образом масса является релятивистским инвариантом, то есть она одна и та же в любой системе отсчёта. Если мы согласимся считать скорость в единицах скорости света, то данную формулу в специальной теории относительности можно упросить до:

Как видно из приведённых формул, релятивистская масса тела растёт с увеличением скорости. Как следствие — по мере приближения к скорости света потребуется всё большая и большая сила для дальнейшего увеличения скорости. Релятивистская масса стала бы бесконечно большой при достижении этого порога, что так же означает, что до придания телу такой скорости, потребуется бесконечно большое усилие.

В общей теории относительности всё ещё больше усложняется, но для нас сегодня m в формуле E = mc² означает массу покоя. Полную же массу можно считать индикатором того, насколько сложно будет придать объекту ускорение, либо какое гравитационное воздействие будет испытывать данный объект.

Вернёмся к примерам, вот ещё один: как только вы включите фонарь, его масса немедленно начнёт уменьшаться. Свет, который исходит от фонаря, уносит энергию, которая ранее была запасена электрохимическим образом в батарее и добавлялась к полной массе фонаря. Наше солнце – в принципе, тот же фонарь, только огромных размеров. Оно теряет около 4 миллионов тонн массы каждую секунду и только его огромные размеры спасают нас от гибели в холоде и тьме, потому что эта масса – лишь 1×10⁻²¹ доля полной массы Солнца (за почти десять миллиардов лет своего существования, Солнце истратило лишь 0,07% своей массы).

Так что же означают слова, что солнце преобразует массу в энергию? Речь не идёт ни о какой алхимии. Вся энергия солнечного света – результат преобразования иной формы энергии – кинетической и потенциальной энергии частиц, из которых состоит наше Солнце. Те 4 миллиона тонн, которые теряет наше Солнце – лишь результат уменьшения потениальной и кинетической энергии частиц, из которых оно состоит.

Всё, что мы взвешиваем на весах – лишь энергия частиц, мы просто никогда этого не замечали.

Ещё пример: представьте, что вы стоите с фонариком в руке внутри закрытого ящика с зеркальными стенками, который, в свою очередь, стоит на больших весах. Уменьшится ли показание весов, если включить фонарик? Ответ – нет, не уменьшится. Хотя масса фонаря и уменьшится, масса всего ящика останется неизменной, так как энергия фотонов, которые покинули фонарик, не покинет пределы ящика, и хотя у фотонов масса покоя отсутствует, их энергия включается в массу покоя ящика.

В каждом из рассмотренных примеров целый объект имел большую массу, чем масса его составных частей, но в начале этого поста было сказано, что масса атома водорода меньше, чем сумма масс протона и электрона, из которых он состоит. Почему так?

Потому что потенциальная энергия может быть и отрицательной. Давайте обозначим потенциальную энергию протона и электрона, находящихся бесконечно далеко друг от друга за нулевую. В силу того, что они притягиваются друг к другу, чем меньше между ними расстояние, тем меньше будет их потенциальная энергия (точно так же, как потенциальная гравитационная энергия уменьшается по мере приближения к поверхности земли). Если они сблизятся до размеров атома водорода, их потенциальная энергия меньше нуля. Хотя электрон в атоме водорода и обладает ещё кинетической энергией, так как он движется вокруг протона, суммарная энергия системы протон-электрон всё равно будет отрицательной, а следовательно, согласно нашей формуле m = E/c² будет так же меньше нуля.

Именно поэтому масса атома водорода меньше, чем сумма масс его составных частей. На самом деле, масса любого атома в периодической таблице будет меньше, чем сумма масс протонов, нейтронов и электронов, из которых они состоят.

То же самое касается и молекул. Молекула кислорода O₂ весит меньше, чем два отдельных его атома, так как суммарная потенциальная и кинетическая энергия этих атомов становится меньше нуля, когда они образуют химическую связь друг с другом.

А что насчёт самих протонов? Они состоят из частиц, называемых кварки, и их суммарные массы примерно в 100 раз меньше массы протона. Так откуда же у протона масса? Она «добирается» из глюонов (или, если упрощённо – потенциальной энергии кварков).

Откуда же берётся масса элементарных частиц (электронов или кварков)? По крайней мере в стандартной модели физики частиц, у них нет составных частей (поэтому они и называются элементарными). С определёной точки зрения (и точки зрения до-Эйнштейновской физики), их массы элементарны, однако, и об их массе можно судить, как о некоей форме потенциальной энергии. Например, можно рассматривать их массу, как потенциальную энергию взаимодействия электронов и кварков с полем Хиггса, а так же с электрическими полями, которые они сами же и порождают, либо, в случае с кварками – потенциальная энергия взаимодейтсвия с их глюонными полями.

Даже классический пример так называемого «преобразования массы в энергию» – аннигиляцию материи и антиматерии концептуально сводится к тому же преобразованию одного вида энергии к другому, и вам не требуется алхимия по преобразованию массы в энергию для его объяснения.

Основная идея данного поста в том, что масса – понятие виртуальное. Это всего лишь свойство, свойство, которое проявляет энергия, поэтому некорректно думать, что масса может являться мерой количества материала в том или ином объекте, на самом деле, это характеристика количества энергии, которой данный объект обладает. Значение именно этой характеристики мы получаем, когда взвешиваем тот или иной объект.

Продолжение. Часть 1, часть 2.

В первой части своего повествования, я упомянул как аксиому тот факт, что скорость света постоянна и не зависит от системы отсчёта, однако, не рассказал, зачем вообще нашей вселенной понадобилось ограничивать максимальную скорость передвижения. Данный пост я хочу посвятить исключительно ответу на вопрос

ЗАЧЕМ ВСЕЛЕННОЙ СКОРОСТЬ СВЕТА И ПОЧЕМУ СВЕТ ЗДЕСЬ НИ ПРИ ЧЁМ?

Имеет ли скорость света какое-либо отношение собственно к свету? Что же делает скорость света такой «специальной», почему мы наблюдаем такой «Вселенский» заговор, препятствующий всем фотонам (да что там фотонам – чему угодно!) перемещаться быстрее, чем предельные 299 тыс. км/с?

Ответ — данное утверждение ложно. Вернее оно перевёрнуто с ног на голову. Вселенная не устроена так, чтобы поддерживать скорость света постоянной, в действительности пространству-времени наплевать на свет, оно и сейчас расширяется быстрее скорости света и при этом ещё и продолжает ускоряться. Вселенское ограничение скорости имеет более глубокие корни.

В предыдущем посте я уже затронул причинность при рассказе о пространственно-временных интервалах. Причинно-следственные связи — это единственное, о чём могут договориться любые наблюдатели, находящиеся в любой системе отсчёта.

Но почему у причинности имеется максимальная скорость? И почему эта скорость случайно совпадает со скоростью света в вакууме?

Давайте разбираться, и начнём мы издалека, с 1632 года, когда Галилео Галилей предстал перед судом Святой Инквизиции за его поддержку в своей книге идей Коперника о гелиоцентрической системе мироустройства. Однако, кроме всего прочего, в своей книге Галилей так же упомянул «принцип относительности», который его словами звучал примерно так:

Галилео заявлял, что не только нет никакого особенного места, но и нет никакой особенной скорости, которая могла бы повлиять на исход «механического эксперимента» в системе, которая движется прямолинейно и без ускорения. Это одно из великих предвидений Галилея было позднее кодифицировано другим гигантом — Исааком Ньютоном в своих «законах».

Перенесёмся на 200 лет позднее для того, чтобы встретить ещё одного героя нашего рассказа – Джеймса Кларка Максвелла, который умудрился вплести эти законы в 4 уравнения, элегантно описывающие весь феномен электромагнетизма.

К концу 19 века у нас были законы Ньютона, уравнения Максвелла, ещё несколько теорий, и общее ощущение того, что физика закончилась и вселенная познана... кроме двух маленьких проблемок — первые намёки на квантовую природу Вселенной и небольшую сумятицу, которые уравнения Максвелла внесли в Галилееву относительность. Вообще, и Ньютонова механика негласно опиралась на предположение, что скорость света бесконечно велика, а если бы это было действительно так, то это повлекло бы весьма серьёзные осложнения, однако, давайте разберёмся с уравнениями Максвелла, вот они:

Эти уравнения настолько значимы, что отлиты в бронзе на его памятнике. Не пугайтесь, примерный смысл этих уравнений выражается следующим образом:

1. Электрический заряд является источником магнитной индукции (теорема Гаусса).

2. Магнитный заряд отсутствует (теорема Гаусса для магнитной индукции)

3. Изменение магнитной индукции порождает вихревое электрическое поле (закон индукции Фарадея)

4. Электрический ток и изменение электрической индукции порождают вихревое магнитное поле (закон Ампера - Максвелла).

Тот перевёрнутый треугольник называется "набла" - это просто индикатор особой операции, чуть сложнее, чем операторы + или —.

Но будем проще. Позовём наших друзей, Алису и Бориса, которые путешествуют на железнодорожной платформе. При этом Алиса ещё катается на скейте... и она электрическая, нам ведь нужно что-то электрически-заряженное, чтобы генерировать магнитное поле. Выглядит это как-то так:

Перемещаясь по платформе, Алиса генерирует магнитное поле, и мы, зная уравнения Максвелла, можем посчитать силу данного поля, зная полную скорость Алисы (v1 + v2). Мы так же можем прямо измерить эту силу при помощи физического эксперимента.

Борис — кот учёный и тоже умеет считать. Наблюдая за перемещениями Алисы со скоростью v1 он так же посчитает силу магнитного поля... и что-то не сходится. Очевидно же, что сила магнитного поля, которое генерирует Алиса, одна и та же. Мы измеряем не само поле, а его эффект — силу Лоренца — зависимый от скорости баланс между электрическим и магнитными полями. Оба поля работа работают, чтобы создать эту силу (полная сила электромагнитного поля на движущийся со скоростью v заряд q, в которую вносит свой вклад как электрическое Е, так и магнитное B поля:

F = q(E + [v × B])

Причём, сила эта не зависит от системы отсчёта. Это наводит нас на мысль о том, что электромагнитная сила каким-то образом связывает скорость и пространство-время. Как же нам выявить эту связь? Борису и нам нужна какое-нибудь волшебное преобразование, позволяющее переводить уравнения Максвелла из одной системы отсчёта в другую.

Таким примером могло бы служить Галилеево преобразование, которое просто говорит о том, что скорости складываются, а пространство и время не зависят от скорости. То же самое преобразование использует Ньютоновская механика, и мы только что применили их для преобразования уравнений Максвелла к скорости Алисы.

x' = x – vt

Но внезапно оказалось, что к уравнениям Максвелла нельзя применить Галилеево преобразование таким образом, чтобы они выдавали непротиворечивые результаты, иными словами они НЕ ИНВАРИАНТНЫ!

Вроде бы они и выдавали правильные значения для низких скоростей, но приводили в полный хаос векторные составляющие полей, а для высоких скоростей эти значения... нет, просто забудьте о высоких скоростях! Физика совсем поломалась!

После преобразований, линии напряжённости магнитного поля будут выглядеть как-то так:

Так что же, Максвелл был неправ? Нет, как выяснилось, неправ был Галилей.

Преобразования, на которых работала Ньютоновская механика, были неправильными. Единственные работающие преобразования, были Лоренцевы (о них я рассказывал в первой части), но до сего момента они были чуть больше, чем некая математическая абстракция для преобразования поворота в четырёхмерном пространстве (к слову, к современному виду их привёл французский математик Анри Пуанкаре за 5 лет до Эйнштейна в 1900 года, который об этой работе не знал и сделал то же самое лишь в 1905).

Лоренцевы преобразования были известны задолго до Эйнштейна. Кому интересно узнать больше, на Википедии есть хорошая статья про то, как их можно вывести самостоятельно в домашних условиях.

Вкратце, история сводится к следующим логическим выкладкам:

Давайте честно признаем, что сложение скоростей (v1 + v2) не работает! Необходимо другое преобразование!

Законы физики работают неизменно, вне зависимости от положения, ориентации или скорости. Нам абсолютно не важно, где находится Алиса, в каком направлении, и с какой скоростью она движется. Это должно быть так — Земля вертится вокруг своей оси, вращается вокруг Солнца, Солнце вращается вокруг центра Млечного пути, наше положение, ориентация и скорость меняются кардинальным образом, в зависимости от нашей точки зрения, но наши физические эксперименты выдают одни и те же результаты, несмотря на это.

Теперь давайте сделаем ещё одно смелое предположение — что Вселенная устроена логично!

Добавим так же требование, что нам постоянно необходимо делать преобразования между разными системами отсчёта туда и обратно и получать непротиворечивые результаты — мы должны иметь возможность пройти путь преобразований при переходе из в системы отсчёта Алисы к системе отсчёта Бориса, затем – в нашу систему отсчёта, откуда мы их наблюдаем, а затем повторить весь путь назад к Алисе и получить те же результаты, с которых мы начали, при этом изменяя лишь один параметр — скорость.

И наконец, добавим ко всему этому щепотку алгебры — получим преобразования Лоренца. Единственное преобразование, которое отвечает всем нашим требованиям!

Эйнштейн заподозрил, что поскольку данные преобразования столь хорошо справляются сзадачей, возможно, они описывают некие фундаментальные законы самой природы пространства-времени, природы нашей реальности.

Однако, в формуле преобразования Лоренца присутствует некая константа c, значение которой нам неизвестно.

Физический смысл этой константы – вселенский скоростной предел. Почему? Потому что без неё константы, преобразования Лоренца бы попросту не работали, данная константа — необходимый элемент формулы преобразования, без которого обойтись невозможно. Преобразования Галилея — это лишь частный случай преобразований Лоренца, гдс c = ∞. И действительно, с точки зрения симметрии и относительности, константа c действительно могла бы быть бесконечной.

При помощи преобразований Лоренца, наконец, позволили получить инвариантные версии уравнений Максвелла (согласованное значение для магнитного поля Алисы, вне зависимости от системы отсчёта: нашей, Бориса, либо её собственной), без них, мы бы не смоли дать описания законам электромагнетизма — это стало ещё одним подтверждением того, что данные преобразования корректно описывают окружающую нас действительность.

Однако, не любое значение константы с нам подойдёт. Данное значение должно быть комбинацией значений фундаментальных констант в уравнениях Максвелла, иными словами, для того, чтобы электрические законы и законы магнетизма работали, нам так же необходимо ограничение — совершенно определённое значение константы c в формуле преобразования Лоренца.

Так что же это за значение? Да можно просто найти его комбинируя результаты физических экспериментов с электромагнитными полями, а затем — применять к этим значениям преобразования Лоренца туда и обратно с разными значениями с. Когда после преобразования из одной системы отсчёта в другую и обратно результаты совпадут с исходными, это и будет требуемым нам значением. Но подождите... ВНЕЗАПНО оказывается, что значение, которое мы нашли, в точности совпадает с измеренной скоростью распространения электромагнитных волн — скоростью света.

Ещё со времён Ньютона мы знаем, что масса обременяет движение, если же у чего-либо отсутствует масса, то нет и никаких препятствий двигаться настолько быстро, насколько это вообще возможно. Фотоны, гравитационные волны, глюоны — всё, что не имеет массы движется в нашей Вселенной с максимально-возможной скоростью. Соответственно, и для передачи информации (взаимодействия) между двумя уголками Вселенной, максимальной скоростью будет являться скорость распространения электромагнитных волн в вакууме.

Иными словами, скорость света, это максимальная скорость распространения причинно-следственных связей — скорость причинности.

Взгляните на рисунок — это трёхмерное представление уже знакомой нам диаграммы Минковского. К нашему настоящему моменту (красная стрелка показывает наблюдателя) из прошлого сужается воронка — наш «световой конус прошлого». На наше текущее настоящее может повлиять только событие, которое попадает в рамки данного конуса — этот конус — наш «горизонт событий». В будущее воронка расходится и включает в себя все события, на которые мы в состоянии повлиять из настоящего момента. Если событие находится за пределами нашего светового конуса, то причинно-следственной связи между такими событиями быть не может.

Интерпретация Эйнштейном ФИЗИЧЕСКОГО СМЫСЛА преобразований Лоренца и дала нам Специальную Теорию Относительности, установив фундаментальную связь между пространством и временем.

Так что бы было, если бы не было этого Вселенского ограничения скорости? Если мы оставим значение c = ∞ (сейчас речь о константе c в преобразованиях, а не о скорости света), то не было бы и массы, так как на создание какой-либо массы потребовалось бы бесконечное количество энергии (E = mc²), во вселенной существовали бы только безмассовые частицы, перемещающиеся на бесконечной скорости.

Существование самого пространства-времени было бы невозможным – с бесконечным замедлением времени и сокращением расстояний до нуля, между событиями отсутствовали бы причинно-следственные связи (вернее, любое бесконечно-удалённое и бесконечно-давнее событие могло бы повлиять на любое событие в бесконечном будущем и наоборот), был бы вселенский хаос — безвременной танец безмассовых частиц в вечном «здесь и сейчас».

Разумеется, мы не могли бы существовать в подобном парадоксе. Для возникновения нашей Вселенной, ей просто необходимо было ограничить максимальную скорость причинно-следственных связей, иначе она попросту не могла бы возникнуть и существовать .

В следующей части мы поговорим об эквивалентности массы и энергии и об истинном смысле формулы E = mc².

Первая часть моей релятивисткой поэмы была посвящена больше инструментам, которые должны помочь нам разобраться с некоторыми аспектами специальной теории относительности (СТО) – диаграммами Минковского и преобразованиями Лоренца. В этой части мы начнём использовать эти инструменты, чтобы разбирать конкретные кажущиеся парадоксы.

Итак, когда мы хотим перемеситься из неподвижной системы отчёта в подвижную или обратно, на помощь нам приходят преобразования Лоренца:

Одним из важных свойств данных преобразований является то, что события, которые в одной системе отсчёта происходили в одно и то же время, вовсе не обязательно будут одновременными в движущейся системе. Это влечёт за собой вывод – события, которые неподвижному наблюдателю кажутся одновременными, не будут являться таковыми для движущегося наблюдателя —

ОДНОВРЕМЕННОСТЬ ОТНОСИТЕЛЬНА!

Иными словами наблюдатели, один из которых неподвижен, а второй движется, никогда не смогут договориться об одновременности каких-либо событий.

На диаграмме внизу видно, как три события A, B и C, которые происходят одновременно для неподвижного наблюдателя (имеют одну и ту же вертикальную временную координату), для движущихся наблюдателей, эти события уже не одновременны, более того, наблюдатети, движущиеся с разной скоростью будут спорить друг с другом так же и порядке их наступления:

Если мы приглядимся к формуле Лоренцева преобразования для скорости, мы увидим, что новая временная координата зависит и от скорости и от первоначального положения события в пространстве. Из-за того, что в знаменателе стоит скорость света в квадрате — астрономическое число (89 875 517 873 681,764 км/с – восемьдесят девять триллионов километров в секунду), при малых скоростях данная часть формулы практически всегда равна 0, однако, при увеличении скорости и расстояния до события до значений, сопоставимых со скоростью света растёт и разница в восприятии временной координаты данного события.

Одними из наиболее удивительных свойств преобразований Лоренца являются релятивистское замедление времени и Лоренцево сокращение. Оба эффекта являются, так или иначе, следствием свойства относительности одновременности.

Давайте разберёмся для начала с замедлением времени.

Предположим, Алиса движется на 33% скорости света, и у неё есть секундомер, которым она отмеряет каждую секунду своего путешествия. Борис остаётся неподвижным, и у него тоже есть секундомер. Алиса смотрит в телескоп на секундомер Бориса, сравнивает его показания со своим секундомером и выясняет, что у Бориса каждая секунда длится примерно на 6% дольше. Эту картину мы наблюдаем на следующей диаграмме, которая показывает, каким мир видит Алиса.

Но тут Борис тоже решил взглянуть через телескоп на секундомер Алисы и сравнить показания. Внезапно оказывается, что это у Алисы часы идут медленнее, чем у него, что мы видим на следующей диаграмме (скорость указана -0,33с).

На самом деле, разбираться, кто из них прав, смысла большого нет, так как оба наших героя забывают об относительности одновременности. Алиса считает, что каждую секунду Бориса, на её часах проходит 1,06 с, она предполагает, что её часы синхронизированы с часами Бориса, однако в её системе отсчёта, это уже не так. Если два секундомера разделяет расстояние L, каждый из наблюдателей будет видеть на часах другого задержку в v * L/c^2 секунд.

Чтобы ещё более наглядно представить себе суть явления замедления времени, давайте сконструируем особые часы, состоящие из двух зеркал, расположенных друг напротив друга, а между ними пульсирует луч света, отражаясь поочерёдно от каждого зеркала, отсчитывая, таким образом, равные интервалы времени. Если мы сядем в космический корабль, разгонимся и будем смотреть на это устройство, то будем наблюдать нечто подобное:

Если же мы отправим данное устройство в полёт, а сами останемся на Земле, то картина, которую мы будем наблюдать, будет уже другой:

Очевидно, что теперь луч света проходит большее расстояние от зеркала до зеркала и, соответственно, длительность каждого импульса будет дольше.

Лоренцево сокращение

Для начала суть: длины движущегося по отношению к нам объекта будут нам казаться короче, чем они есть.

Предположим, у нас есть движущийся стержень определённой длины. Мы измеряем стержень, двигаясь вместе с ним, в его собственной системе отсчёта (на диаграмме – отрезок OB), затем повторяем измерение из неподвижной системы отсчёта (получаем отрезок OC). Как видим из эксперимента, длина движущегося стержня в неподвижной системе отсчёта будет короче.

Невольно может возникнуть вопрос: а какая же длина истинна? Правильного ответа на данный вопрос не существует. Вернее, оба варианта – правильные. Длины в нашем мире относительны, поэтому ответ на данный вопрос требует уточнения – в какой системе отсчёта?

Корни данный феномен берёт всё так же – из относительности одновременности. Сам факт измерения длины предполагает вычисления разности пространственных координат начала и конца стержня, причём эти координаты должны быть взяты ОДНОВРЕМЕННО. Однако, как мы уже поняли, в нашем мире два события, произошедшие одновременно для одного наблюдателя, вовсе не будут одновременными для другого.

А что же сам свет? Давайте подставим в формулы преобразований Лоренца скорость света. Строго говоря, нам это не удастся из-за коэффициента гамма:

Как видно, если мы подставим в качестве v скорость света, весь знаменатель обратится в ноль, а на ноль делить нельзя иногда можно.

С математической точки зрения, данное выражение будет лишено смысла, однако физически сам свет (и любые безмассовые частицы) перемещается в вакууме, не испытывая течения времени вообще. Более того, для фотона света так же не существует и расстояний, так как любое расстояние для него равно нулю. Для фотона света существует только постоянное здесь и сейчас.

Сложение скоростей

Предположим, у нас есть пистолет, который стреляет удивительно-быстрыми пулями на скорости 60% световой. Если мы построим диаграмму подобного выстрела, то она будет выглядеть следующим образом:

Предположим теперь, что мы произвели выстрел из того же пистолета, но при этом мы сами уже двигались на скорости 50% световой. Классическая механика подсказывает нам, что для нахождения скорости пули относительно неподвижного наблюдателя, необходимо сложить нашу скорость 0,5 с и скорость пули 0,6 с, что в сумме даст 110% скорости света.

Однако, в действительности сложение скоростей работает, разумеется не так, в чём легко убедиться, если мы сдвинем ползунок скорости до 0,5 с:

Как мы видим, пуля по-прежнему летит быстро, но по-прежнему не превышает скорость света (жёлтая линия, проходящая под 45° к основным осям). В релятивистской механике сложение скоростей так же зависит от скорости света и считается по формуле:

где v1 и v2 – скорости складываемых объектов. Так, скорость нашей пули в движущейся системе отсчёта будет примерно равна (0,5 + 0,6) / (1 + 0,3) = 1,1 / 1,3 или 84,6% скорости света (как видите, применение коэффициентов скорости света вместо стандартных единиц измерения скорости значительно упрощает расчёты).

Рассмотренные примеры могут навести на мысль, что всё субъективно. Если два наблюдателя в разных системах отсчёта не могут договориться ни о расстоянии до какого-либо события, ни о времени его наступления, ни даже о хронологии наступления двух разных событий, то что же останется объективно?

Оказывается, есть характеристика, с которой согласятся все наблюдатели в любой точке вселенной, с какой бы скоростью относительно друг друга они не двигались. Эта характеристика называется пространственно-временным интервалом между событиями.

Даже если два наблюдателя движутся с разными скоростями и измеряют разные расстояния и временные интервалы между двумя наблюдаемыми событиями, пространственно-временной интервал между ними для обоих будет одним и тем же.

Раз пространственно-временной интервал между событиями универсален для всех наблюдателей, возможно, он что-то значит?

Как мы видим из формулы, знак минус означает, что интервал может быть нулевым, положительным и отрицательным.

Если интервал положительный, то события никак не могут повлиять друг на друга, хотя разные наблюдатели могут и не соглашаться в их хронологии. Если же интервал нулевой или отрицательный, то сигналы одного события могут влиять на сигналы другого.

И так, мы видим, что знак пространственно-временного интервала отвечает на вопрос, могут ли два разных события повлиять друг на друга или не могут. Иными все наблюдатели соглашаются с причинностью двух событий.

Эта идея может идти вразрез с нашей интуицией, так как обычно, когда мы рассуждаем о причинности, мы думаем, что причинность определяется временем, однако, это не так, в действительности же время определяется причинностью.

Формула пространственно-временного интервала напомнила Герману Минковскому в своё время формулу расстояния в 4D пространстве и именно тогда у него возникла идея о том, что наша реальность – это не эволюционирующее во времени трёхмерное пространство, а четырёхмерное пространство-время, а точки в нём – события, а его неевклидова геометрия – единственное, что можно назвать объективно реальным.

Наша жизнь в данном пространстве – это мировая линия с точками рождения и смерти со своими пространственно-временными координатами. Мы воспринимаем реальность, будто мы двигаемся вдоль этой мировой линии, однако, на самом деле, мы – и есть эта линия. Наше будущее не просто предопределено – оно уже существует.

На этой оптимистичной ноте разрешите закончить вторую часть своего повествования. В третьей части мы продолжим рассматривать теорию относительности, для закрепления материала рассмотрим распространённые парадоксы с ней связанные, а так же поговорим о том, почему термин скорость света – это вовсе не про свет (или не только про свет).

P.S. В процессе работы над данным постом для подготовки некоторых иллюстраций, мне пришлось на(говно)кодить небольшую программку под Windows, где можно размещать на пространственно-временных диаграммах  различные события и смотреть, что с ними происходит в разных системах отсчёта. Если кому-то интересно поиграться, вот ссылка на неё на Github.