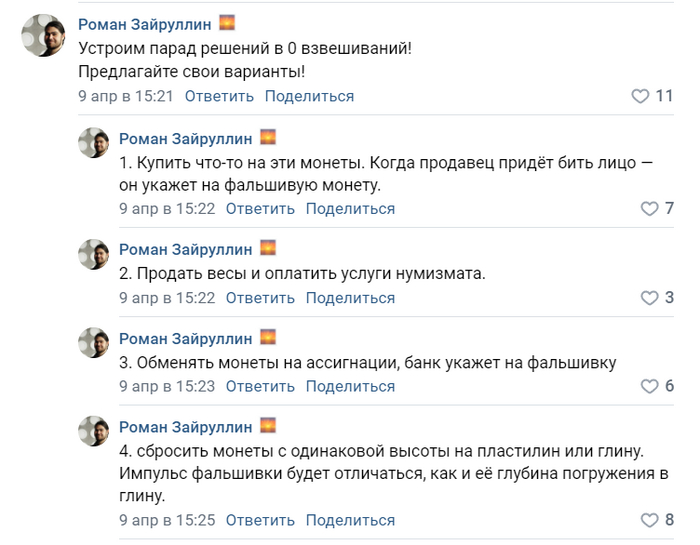
Ответ на пост «Парад решений»
Если мы не знаем, легче или тяжелее монета, то 4 взвешивания.
1. Делим на три группы по 4 монеты, взвешиваем, допустим у нас одна группа отличается по весу
2. Заменяем одну из групп монет на весах, теперь мы точно знаем группу с фальшивой монетой и 8 настоящих монет.
3. Берём две настоящие монеты и две из группы с фальшивой, теперь мы точно знаем 10 настоящих монет
4. Остаётся взять из группы с фальшивой монетой одну и взвесить с настоящей монетой
Тут есть допущение, что если при первом взвешивании группы окажутся одинаковой массы, тогда второе взвешивание окажется ни к чему и хватит трёх.
Если известна вводная на счёт веса (тяжелее или легче), то достаточно трёх взвешиваний.
Пока писал этот коммент понял, что есть способ почти всегда за три взвешивания узнать где фальшивая, даже без вводной.
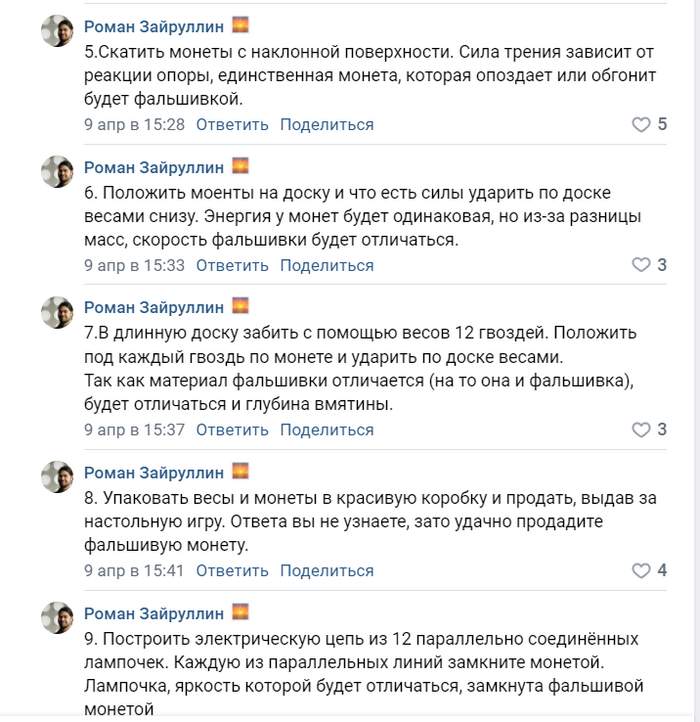
1. Делим на 4 группы по три монеты, взвешиваем, таким образом мы определяем 6 настоящих монет.
2. Заменяем ОДНУ группу монет, таким образом мы вычислим группу из трёх монет с фальшивой монетой.*
3. Взвешиваем две монеты из группы с фальшивой. И вот тут у меня случилась загвоздка. Допустим, в предыдущих двух взвешиваниях весы показывали одинаковый вес, а на третьем разный. Тогда нам понадобится ещё одно взвешивание, чтобы точно определить фальшивую.
Так что вариант хороший, но не идеальный.
*На всякий случай поясню, если весы показали одинаковый вес и после замены снова показали одинаковый вес, то группа с фальшивой, это последняя, если вес разный, то это та, на которую заменили. Если изначально весы показали разный вес и при замене снова разный, то значит фальшивая монета оставалась на весах, а если вес одинаковый, то фальшивую монету только что убрали с весов.