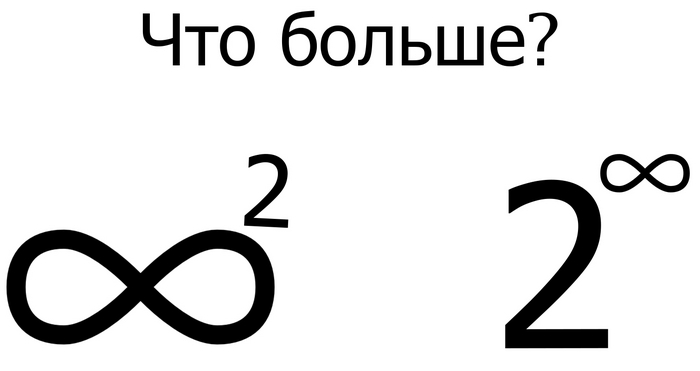
Ответ на пост «Дал chatgpt и аналогам сложную математическую задачу на бесконечность! Чат gpt победит людей(»
Для справки. Правильный ответ был бы примерно такой:
Бесконечность не является числом, поэтому в строгой записи такие выражения встречаться не должны. Попытаемся угадать, что имел в виду спрашивающий.
Если речь идёт о бесконечно больших функциях/последовательностях
a_i -> ∞ и b_i -> ∞,
и мы ищем предел квадрата (a_i)^2 и показательной функции 2^b_i, то оба эти предела равны бесконечности, то есть и (a_i)^2, и 2^b_i - бесконечно большие последовательности. Но это не позволяет сравнить сами последовательности (a_i)^2 и 2^b_i.
Если же квадрат и показательная берутся от одной и той же последовательности, то (a_i)^2 возрастает медленнее, чем 2^a_i, то есть в некотором смысле ∞^2 < 2^∞.
Также вопрос мог подразумевать теоретикомножественный подход. В таком случае, как и в случае с пределами, надо понять, одинаковые ли бесконечности имеются в виду в выражениях ∞^2 и 2^∞. В теории множеств не принято использовать значок ∞.
Если имеются в виду одинаковые бесконечности, например ℵ₀, то из теоремы Кантора и того факта, что любое бесконечное множество равномощно своему декартову квадрату, следует, что
∞^2 < 2^∞
Разумеется, для разных бесконечностей это неверно, например
c^2 = 2^ℵ₀.