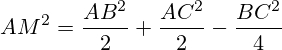Ответ на пост «Алгебра или черчение по поводу»
Чувак, прости Христа ради! Мой прошлый ответ говно. Разумеется, тогда бы все равносторонние треугольники имели бы хоть одну натуральную медиану. И хотелось бы мне заявить теперь, что у равносторонних треугольников не может быть натуральной медианы, да вот прахом труд, о чем псто. При помощи логики, лексики и компьютерного моделирования грубым перебором, мне удалось выяснить теорему:
1. Чтобы в треугольнике с натуральными сторонами все медианы были натуральными он обязан быть подобен треугольнику в котором сумма сторон противолежащих медиане была равна длине иссекаемой ей стороны.
2. Все длины сторон будут четными.
Я теперь могу провернуть этот фокус для любых треугольников. Например выберем число 42, как смысл вселенной, жизни и всего такого.
42 - сторона ab
Я хочу чтобы ac стала равна 58
Океюшки. Иссекаемая сторона всего лишь 42+58 и будет 100
Медиана в таком случае ровно 8, она натуральна. Попробуем колдануть и иссечь сторону bc.
Охренеть! Ее медиана будет 71. Опять натуральное. Отличненько, это и следует из формулы.
0. Очевидно, что только четное число даст четный квадрат
1. Только четное число при делении на два остается натуральным.
2. Иссекаемую сторону мы делим полопам, как алгебраически, так и геометрически. Представим все как
sqrt((2a^2+2b^2-c^2)/2)
При вытряхивании квадратного корня мы это все приведем к виду
sqrt(2a^2+2b^2-c^2)/sqrt(2)
Как много чисел при делении на корень из двух, чертово число, тить его за ногу, дадут натуральные? Только кратные корням из двух. Вроде вот и разобрались.
А теперь вопрос уже к общественности. ЧТО. ЗА. ХУЙНЯ?
ab = 170
ac = 174
bc = 136
m1 = 158
m2 = 127
m3 = 131
ВСЕ медианы данного числа натуральны. Это разрушает мой мозг. Треугольник в гробу видел теорему ab+ac=bc. Да, они принадлежат множеству четных чисел. Это немного успокаивает.