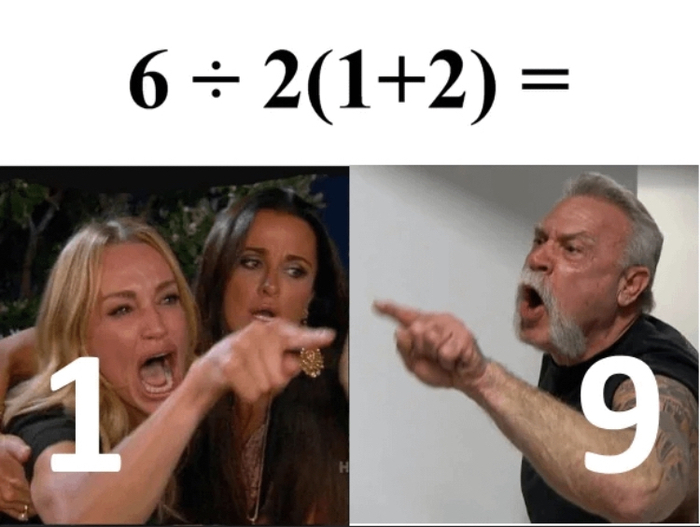Ответ на пост «В 1912 году выпущена книга Принципы математики, люди в 2023 году»
По мере усложнения выражений и отхода от задачек на вычисление выражений часть ребят усваивают подход, мало где подробно описанный, зато понятный специалистам.
Типа использования косой дроби, чувства, когда стоит применять скобки в выражениях вроде cos2x, а когда не нужно, умения отличать степень -1 от знака обратной функции, штриха производной от штриха другой переменной... К таким навыкам относится и понимание тонкостей использования умножения без знака.
Да и не только отсутствие знака может поменять приоритет. Любой адекватный математик поймет запись
a⧸2·b
как a/(2·b), несмотря на знак умножения. Но в учебниках не сказано, что длинная дробь чем-то отличается от короткой, просто опытный человек понимает, что длинной её нарисовали не просто так.
Те, у кого математика так и осталась на уровне младшей школы, подрастают и начинают смеяться: "Вот дураки, нас во втором классе такому не учили".
Чтобы не быть голословным, вот некоторые книги, где прямо говорится про более высокий приоритет умножения путем опускания знака:
В. В. Репьев, Методика преподавания алгебры в восьмилетней школе. Пособие для учителей. - М.: Просвещение, 1967
Вообще, согласия насчет того, как трактовать выражения даже со значками:
a : b · c
- не было в XIX веке, а в начале XX века вышел ряд рекомендаций (например, касательно английского школьного образования - в 1917 году), по которым следует избегать подобных выражений. Об этом вы можете прочитать в F. Cajori, A History of Mathematical Notations, 1929.
Более высокий приоритет умножения без значка, чем у умножения со значком и у деления, реализован в некоторых инженерных калькуляторах, например Casio:
За ссылки спасибо комментарию #comment_146484587